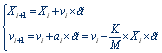|
نانو دانش و فنون مقياس نانو
آنچه از اين فصل ميآموزيم:
1. آشنايي با حرکت
نوساني و پايداري سيستمهاي واقعي؛
2. آشنايي با نوسانگر
هماهنگ و معادلات آن؛
3. مفهوم ناپايداري در
الگوريتم اويلر.
بسياري از حركتهاي
موجود در اطراف ما رفتوبرگشتي هستند، مثل دوران
سيارات به دور خورشيد، يا حركت پاندول ساعت. يكي از
مهمترين حركتهاي نوساني، حركات رفتوبرگشتيِ اتمهاي
يك جامد حول يك نقطة تعادل است كه اصليترين علتِ
ازهمنپاشيدن جامدات است. از اين به بعد، «نپاشيده
شدن» يك جسم براي زمانهاي قابل لمس (مقيد بودن ذرات
به هم در يك شكل واحد در زمانهاي طولاني) را
«پايداري» (باقي ماندن جسم در وضعيت هميشگيش)
ميناميم.
شكل زير نمونهاي ساده
از پايداري (قسمت بالا) و عدم پايداري (قسمت پايين)
ذرهاي تحت اثر جاذبة زمين را نشان ميدهد:
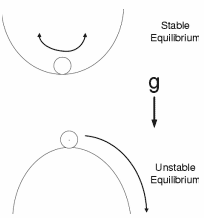
توجه کنيم که وقتي جسمي
ميخواهد در يک مسير يا وضعيت خاص باقي بماند، دو حالت
دارد: يا در يک نقطه نسبت به مرجع ثابتي در حال سکون
است، يا در اطراف آن نقطه اندکي رفت و برگشت دارد. در
هر يک از اين دو حالت جسم داراي حرکت پايدار است.
از طرفي ارتباط رياضي
بين حرکت رفت و برگشتي حول يک نقطه شكل موجي دارد.
به كمك آزمايش شكل 2 ميتوان به موجي بودن حركت
رفتوبرگشتي يك جسم آويزانشده از يك فنر پي برد:
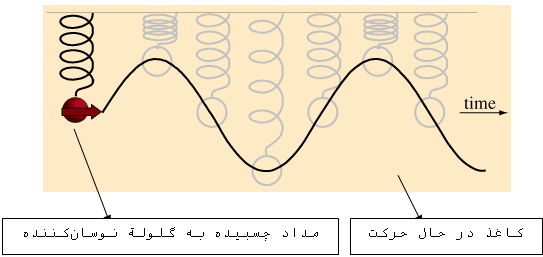
احتمالاً اين آزمايش را
در کتابهاي دبيرستاني ديدهايد.
با اين مقدمه، بررسي
شبيهسازي اين سيستم فوقالعاده ساده ولي حياتي را
آغاز ميكنيم.
براي فنري كه تنها در
جهت افقي روي يك سطح بدون اصطكاك در حال نوسان است،
قانون دوم نيوتن چنين نوشته ميشود:
(1) 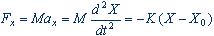
كه K ثابت فنر (ميزان
فشردگي فنر به ازاي نيروي يكنيوتني)، به سفتي فنر
مربوط است (هرچه فنر سفتتر، ثابت فنر بزرگتر). X0 نيز
محل تعادل فنر، يعني جايي كه به ذرة متصل شده هيچ
نيرويي وارد نميشود، يا به عبار ديگرF(x0)=0
است. در شكل زير نمايي از آنچه قصد شبيهسازياش را
داريم، ميبينيد.
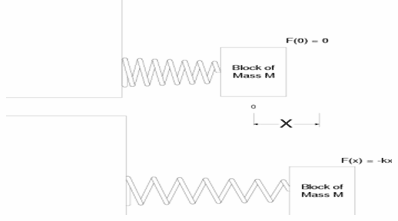
براي راحتي محل تعادل را
صفر ميگذاريم. از رابطة بالا داريم:
(2) 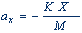
بنابراين، در اين مسئله
الگوريتم اويلر كه در بخش
دوم معرفي
شد، بدين صورت نوشته ميشود:
(3) 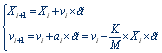
باز هم با داشتن دو
مقدار اوليه براي سرعت و مكان ميتوان به حل رايانهاي
اين مسئله پرداخت. توجه كنيم كه هر بار X,V محاسبه
شدند، a هم بايد محاسبه شود. البته اينجا مقادير K,M
نيز بايد تعيين شوند كه در محاسبات حاضر نسبت √K/M را
ω0 گذاشته
و ميتوانيم به آن مقادير دلخواهي را نسبت دهيم كه
براي يک جرم ثابت، هرچه مقدار آن از 1 بزرگتر شود فنر
سفتتري داريم.
دربارة جواب واقعي اين
مسئله احتمالاً دانشآموزان حدس توابع نوساني را
انتخاب خوبي ميدانند:
(4) 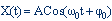
كه در آن، مقادير A و ω0
و 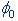 به
ترتيب به دامنة نوسانات فنر، تعداد نوسانات در يک
ثانيه (ضرب در عدد پي) و محل اولية شروع نوسان
وابستهاند. اين جوابِ واقعيِ شکل کسينوسي نوسانگر
يکبُعدي است. به
ترتيب به دامنة نوسانات فنر، تعداد نوسانات در يک
ثانيه (ضرب در عدد پي) و محل اولية شروع نوسان
وابستهاند. اين جوابِ واقعيِ شکل کسينوسي نوسانگر
يکبُعدي است.
در جدول 1-4 يک دسته مقادير لازم براي شبيهسازي را
فهرست کردهايم.
|
100 واحد
(ميليمتر ) |
A، دامنة
نوسانات |
|
5 راديان بر
ثانيه |
ω0=
√K/M، جرم را واحد فرض کنيد. |
|
صفر راديان |
 |
از رياضيات و حدس فيزيکي
براي مسئلة نوساني ميتوان به کسينوسي بودن جواب واقعي
مسئله پي برد. جواب مسئله با در نظر گرفتن مقادير جدول
بالا چنين است:
(5) 
از مثلثات مقدماتي
ميدانيم كه دورة (Period) تناوب چنين تابعي (يا
26/1ثانيه) است. (چرا؟)
شکل بالا جواب واقعي
مسئله در چهار دورة تناوب اول است. دقت کنيد که دامنة
نوسانات همواره 100 و ثابت است.
کُد مورد استفاده با طراحي يک دکمه در VB چنين است:

برنامه را از اينجا داونلود كنيد
اگر گام زماني 0.05 را
انتخاب کنيد، به نتيجة زير خواهيد رسيد. پس از دو دوره
تناوب، دامنة نوسانات از مقدار 100 منحرف ميشود.
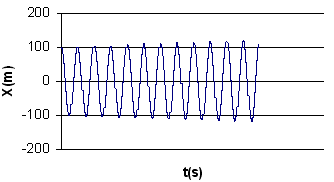
براي گام زماني0.1 اوضاع
بدتر است:

شکل زير نمودار بالاست
پس از زمانهاي بيشترِ نوسان.
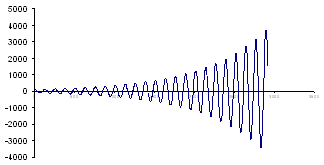
به اين اتفاق «ناپايداري
الگوريتم» گفته ميشود. اين ناپايداري مشابه رياضيِ
ناپايداري است که در قسمت دوم شکل اول اين فصل ميبينيد،
يعني خارج شدن از وضعيتي که ذره همواره ميبايست داشته
باشد، با اين تفاوت كه ناپايداري در آن شکل، ناشي از
طبيعت سيستم بوده، ولي ناپايداري در اينجا ناشي از دقت
كم محاسبات است نه طبيعت نوسانگر.
جالب است بدانيم که در
طبيعت اگر نوسانگري واقعاً اينچنين ناپايدار شود، به
طوري که دامنهاش مدام بزرگ و بزرگتر شود، انرژي
هنگفتي به وجود خواهد آمد. اين پديده «تشديد» نام دارد.
درمورد پديده تشديد نشاني زير را ببينيد:
http://monet.physik.unibas.ch/~elmer/pendulum/nonres.htm#super
مثال بارز تشديد، لشگر
سربازان در حال رژه روي پل متصل به طنابي است که باعث
نوسانات شديد پل و بالاخره پاره شدن آن ميشود!
اگر به تمرين
7 از بخش دوم پاسخ
داده باشيد، خواهيد فهميد كه چرا اين اتفاقات افتاده
است:
هنگامي كه از يک خط با
شيب ثابت براي رسيدن به نقطة بعدي مکان استفاده ميكنيم،
مقادير بهدستآمده از روش عددي، بهتدريج با زياد شدن
فاصلة نقطة دوم، از مقادير واقعي دور ميشود. شکل زير
نشانگر اين موضوع است. در بخشهاي بعدي دوباره به اين
موضوع بازخواهيم گشت:
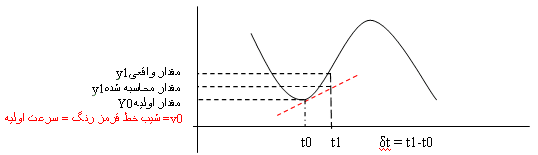
از شکل بالا ميبينيم که
اين الگوريتم براي گامهاي زماني بزرگ در مسئله چندان
مناسب نيست.
براي آنکه تخميني از خطاهاي بهوجودآمده در مسئله
داشته باشيم، سادهترين راه آن است که تفاضل مقدار
واقعي و مقدار شبيهسازي را بر مقدار واقعي تقسيم کنيم.
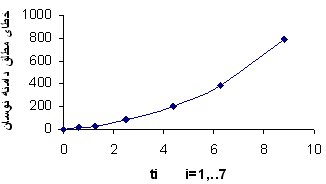
جدول زير بعضي مقادير خطا را براي گام زماني 0.1 نشان
ميدهد:
|
مقدار واقعي |
مقدار شبيهسازي |
زمانti |
درصد خطاي نسبي |
|
100 |
100 |
0 |
0 |
|
100- |
117.124- |
5/  نصف
يک دوره تناوب نصف
يک دوره تناوب |
17.124درصد |
|
100 |
132.87 |
5/ 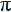 2
يک دوره تناوب 2
يک دوره تناوب |
32.87
درصد |
|
100 |
187.32 |
5/ 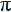 4دو
دوره تناوب 4دو
دوره تناوب |
87.32
درصد |
|
100- |
300.079- |
5/ 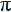 7
سه ونيم دوره تناوب 7
سه ونيم دوره تناوب |
200.79
درصد! |
|
100 |
480.181 |
5/ 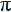 10
پنج دوره تناوب 10
پنج دوره تناوب |
380.181درصد! |
|
100 |
892.91 |
5/ 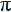 14
هفت دوره تناوب 14
هفت دوره تناوب |
792.91درصد!!! |
نمودار زير از جدول بالا
ساخته شده است.
در فصل بعد بهتفصيل يک
دسته الگوريتم پايدار را معرفي ميكنيم و به بحث خطاها
توجه بيشتري مينماييم.
تمرين
1. نتايج مندرج در
نمودارهاي بالا را با استفاده از برنامهاي كه در
انتهاي متن آمده است، به دست آوريد.
2. با توجه به معادلات 3
و 5 جواب واقعي سرعت و جواب عددي سرعت با گامهاي
زماني فوقالذکر را ترسيم کنيد. آيا سرعت مانند مسئلة
سقوط آزاد هيچ خطايي ندارد؟
3. شتاب نوسانگر نسبت به
زمان از رابطة 2 به دست ميآيد. براي گام زماني 0.1 آن
را ترسيم نماييد.
5. انرژي کل نوسانگر
سادة يکبُعدي اينگونه تعريف ميشود:
(6) 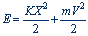
الف ـ نشان دهيد که
مقدار ثابت اين انرژي 0.125
ژول است. (به کمک جدول 1-4 اين فصل)
ب ـ با افزودن چند خط به
برنامه، منحني انرژي را نسبت به زمان ترسيم کنيد. آيا
انرژي ثابت ميماند؟ چرا؟
6ـ چگونه ميتوان تخميني
از ميزان انحراف از جواب واقعي داشت؟ مثلاً حدس زد که
پس از 4 دورة تناوب، ميزان خطا چقدر است. به کمک جدول
2-4 و مقدار گام زماني مربوطهاش، آيا ميتوانيد قاعدهاي
کلي براي انتشار خطا بيابيد؟
7. مقادير جدول 1-4 را
به مقادير زير تبديل و نمودارهاي اين فصل را تکرار
کنيد.
|
100 واحد (ميليمتر
يا ميکرومتر) |
A دامنة
نوسانات |
|
10 راديان
بر ثانيه |
ω0=
√K/M، جرم را واحد فرض کنيد. |
|
 راديان راديان |
 |
تمام اتفاقات جديد را
ذکر کنيد.
8. اگر فنر از سقف
آويزان شده باشد، نتايج چگونه تغيير خواهند کرد؟
9. ثابت کنيد سرعت اوليه
را با داشتن مکان اوليه و فاز اوليه ميتوان به صورت
زير حساب کرد
باشگاه نانو
نانوفناوري محاسباتي قسمت اول
نانوفناوري محاسباتي قسمت دوم
نانوفناوري محاسباتي قسمت سوم
نانوفناوري محاسباتي قسمت چهارم
|