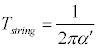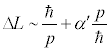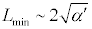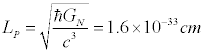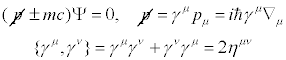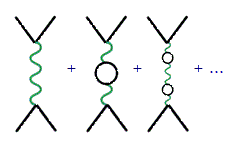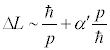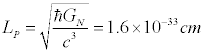|
رشته سیمهای گیتار را تصور کنید که با کشیده شدن در طول گیتار
کوک شدهاند؛ بسته به آنکه سیمها چقدر کشیده شوند و تحت فشار
قرار گیرند، نتهای موسیقی مختلفی بوسیله آنها ایجاد میشود.
میتوانیم این نتهای موسیقی را
"حالتهای برانگیخته" سیمهای
گیتار تحت کشش بنامیم.
به طور مشابه در
تئوری ریسمان ذرات بنیادین که در شتابدهندهها مشاهده میشوند
را میتوانیم نتهای موسیقی و یا همان
"حالتهای برانگیخته" فرض
گنیم. در
تئوری ریسمان همانند نواختن گیتار، ریسمانها باید تحت کشش قرار
بگیرند تا برانگیخته شوند. اگرچه ریسمانها در تئوری ریسمان در
فضا-زمان شناور هستند و مانند گیتار مقید نیستند ولیکن با این
حال آنها کشش دارند، کشش ریسمان در تئوری ریسمان همانطور که در
قبل گفتیم با کمیت
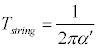
شناخته میشود
و در آن 'α با
مربع مقیاس طول ریسمان متناسب است.
اگر تئوری
ریسمان تئوری گرانش کوانتوم باشد، پس متوسط اندازه ریسمان باید
چیزی نزدیک به مقیاس طول گرانش کوانتوم باشد که طول پلانک
نامیده میشود و حدود 10-33 سانتیمتر
میباشد. متاسفانه این بدان معناست که ریسمانها به حدی برای
دیدن با تکنولوژی فعلی فیزیک ذرات کوچک هستند که فیزیکدانان
مجبور به ابداع روشهای جدیدی برای آزمایش تئوری شدند.تئوری در
ابتدا فقط برای بوزونها بود، به منظور اینکه فرمیونها هم
وارد تئوری ریسمان شوند باید یک نوع بخصوص از تقارن به نام
ابرتقارن وجود میداشت که به واسطه آن برای هر بوزون، یک
فرمیون متناظر وجود داشته باشد. پس ابرتقارن، ذرات حامل نیرو و
ذراتی که ماده را میسازند به هم مربوط میکند.
نتایج ابرتقارن
در آزمایشات ذرات مشاهده نشدهاند اما تئوریستها معتقد هستند
که ذرات ابرتقارن بزرگتر و سنگینتر از آن هستند که در
شتابدهندههای فعلی بتوان آنها را مشاهده کرد. ایجاد
شتابدهندههای قویتر انرژی بالا در دهه آینده میتواند شواهد
لازم برای ابرتقارن در اختیار ما قرار دهند.
مهم نبود که هر
کس چقدر تلاش میکرد، به نظر میرسید گرانش به هیچ وجه به
نظریهای قابل بهنجارش تبدیل نمیشود؛ یک مشکل بزرگ این بود که
امواج گرانش کلاسیک که فرض میشد ذره حامل آن گراویتون است،
دارای اسپین 2 بودند و برای اسپین 2 ، عبارت 4j-8+D مساوی D میشد
و برای D=4 ،
انتگرال بینهایت میشد، مثل توان چهارم ممنتوم وقتی که ممنتوم
به سمت بینهایت میل میکند[D تعداد
بعد است و ما در جهان ما 4 بعدی است.]. این
برای فیزیکدانان غیرقابل هضم بود و سالها تلاش آنها در راه
رسیدن به "گرانش کوانتوم" ناکام ماند.در اینجا بود که تئوری
ریسمان وارد شد تا این خلا را پر کند.
تئوری ریسمان در
اصل برای توصیف روابط میان جرم و اسپین هادرونها پیشنهاد شده
بود. در تئوری ریسمان، ذرات از برآشفتگی ریسمانهای بسیار
ریزی بوجود میآمدند ؛ یک ذره که از این برآشفتگیها بر
میخواست، ذرهای بود با جرم صفر و دو واحد اسپین. موفقیتی
که تئوری ریسمان داشت این بود که در مدل دیاگرامهای فاینمن،
دیاگرامها به سطوح صاف دو بعدی تبدیل میشدند و انتگرالهای روی
سطح دیگر مشکل فاصله صفر را نداشتند.
تئوری ذرهای :
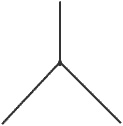
تئوری ریسمان :

در 1974 نهایتا این سوال
مطرح شد که " آیا تئوری ریسمان میتواند تئوری گرانش کوانتوم
باشد؟ ". در
تئوری ریسمان، ممنتوم بینهایت به معنای فاصله صفر نبود، زیرا
در این تئوری رابطه بین ممنتوم و فاصله به قرار زیر بود:
کمیت 'a به
تنش ریسمانها بستگی داشت ، کمیتی بنیادین بر اساس رابطه :
رابطه بالا به طور
غیرمستقیم بیان میکند که کمترین طول قابل مشاهده برای تئوری
ریسمان به صورت زیر است:
رفتار ذره در فاصله صفر
که در تئوری میدان کوانتوم بسیار مشکلساز بود، در تئوری
ریسمان بسیار بیاهمیت شد و همین باعث شد که تئوری ریسمان
نامزد تئوری گرانش کوانتوم شود. اگر
تئوری ریسمان ، تئوری گرانش کوانتوم باشد، مقدار طول مینیموم
باید حداقل اندازه طول پلانک باشد که از ترکیب ثابت پلانک و
ثابت گرانش نیوتون و سرعت نور بدست میآید:
اگرچه مساله مقیاس طول در تئوری ریسمان به خاطر دوگانگی ریسمانها
پیچیده و مشکل شد.
111
مراکز
سازمان ملی پرورش استعدادهای درخشان ایران
What
is String Theory
Relativistic
quantum field theory has worked very well to describe the
observed behaviors and properties of elementary particles. But
the theory itself only works well when gravity is so weak that
it can be neglected. Particle theory only works when we pretend
gravity doesn't exist.
 General
relativity has yielded a wealth of insight into the Universe,
the orbits of planets, the evolution of stars and galaxies, the
Big Bang and recently observed black holes and gravitational
lenses. However, the theory itself only works when we pretend
that the Universe is purely classical and that quantum mechanics
is not needed in our description of Nature. General
relativity has yielded a wealth of insight into the Universe,
the orbits of planets, the evolution of stars and galaxies, the
Big Bang and recently observed black holes and gravitational
lenses. However, the theory itself only works when we pretend
that the Universe is purely classical and that quantum mechanics
is not needed in our description of Nature.
 String
theory is believed to close this gap. String
theory is believed to close this gap.
 Originally,
string theory was proposed as an explanation for the observed
relationship between mass and spin for certain particles called
hadrons, which include the proton and neutron. Things didn't
work out, though, and Quantum
Chromodynamicseventually
proved a better theory for hadrons. Originally,
string theory was proposed as an explanation for the observed
relationship between mass and spin for certain particles called
hadrons, which include the proton and neutron. Things didn't
work out, though, and Quantum
Chromodynamicseventually
proved a better theory for hadrons.
 But
particles in string theory arise as excitations of the string,
and included in the excitations of a string in string theory is
a particle with zero
mass and two units of spin. But
particles in string theory arise as excitations of the string,
and included in the excitations of a string in string theory is
a particle with zero
mass and two units of spin.
 If
there were a good quantum theory of gravity, then the particle
that would carry the gravitational force would have zero
mass and two units of spin.
This has been known by theoretical physicists for a long time.
This theorized particle is called thegraviton. If
there were a good quantum theory of gravity, then the particle
that would carry the gravitational force would have zero
mass and two units of spin.
This has been known by theoretical physicists for a long time.
This theorized particle is called thegraviton.
 This
led early string theorists to propose that string theory be
applied not as a theory of hadronic particles, but as a theory
ofquantum
gravity,
the unfulfilled fantasy of theoretical physics in the particle
and gravity communities for decades. This
led early string theorists to propose that string theory be
applied not as a theory of hadronic particles, but as a theory
ofquantum
gravity,
the unfulfilled fantasy of theoretical physics in the particle
and gravity communities for decades.
 But
it wasn't enough that there be a graviton predicted by string
theory. One can add a graviton to quantum field theory by hand,
but the calculations that are supposed to describe Nature become
useless. This is because, as illustrated in the diagram above,
particle interactions occur at a single point of spacetime, at
zero distance between the interacting particles. For gravitons,
the mathematics behaves so badly at zero distance that the
answers just don't make sense. In string theory, the strings
collide over a small but finite distance, and the answers do
make sense. But
it wasn't enough that there be a graviton predicted by string
theory. One can add a graviton to quantum field theory by hand,
but the calculations that are supposed to describe Nature become
useless. This is because, as illustrated in the diagram above,
particle interactions occur at a single point of spacetime, at
zero distance between the interacting particles. For gravitons,
the mathematics behaves so badly at zero distance that the
answers just don't make sense. In string theory, the strings
collide over a small but finite distance, and the answers do
make sense.
 This
doesn't mean that string theory is not without its deficiencies.
But the zero distance behavior is such that we
can combine quantum mechanics and gravity,
and we can talk sensibly about a string excitation that carries
the gravitational force. This
doesn't mean that string theory is not without its deficiencies.
But the zero distance behavior is such that we
can combine quantum mechanics and gravity,
and we can talk sensibly about a string excitation that carries
the gravitational force.
 This
was a very great hurdle that was overcome for late 20th century
physics, which is why so many young people are willing to learn
the grueling complex and abstract mathematics that is necessary
to study a quantum theory of interacting strings. This
was a very great hurdle that was overcome for late 20th century
physics, which is why so many young people are willing to learn
the grueling complex and abstract mathematics that is necessary
to study a quantum theory of interacting strings.

Once special relativity was on firm observational and
theoretical footing, it was appreciated that the Schrödinger
equation of quantum mechanics was not Lorentz invariant,
therefore quantum mechanics as it was so successfully developed
in the 1920s was not a reliable description of nature when the
system contained particles that would move at or near the speed
of light.
The problem is that the Schrödinger equation is first order
in time derivatives but second order in spatial derivatives. The
Klein-Gordon equation is second order in both time and space and
has solutions representing particles with spin 0:
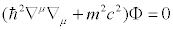
Dirac came up with "square root" of Klein-Gordon equation using
matrices called "gamma matrices", and the solutions turned out
to be particles of spin 1/2:
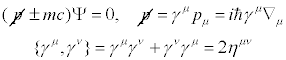
where the matrix hmn is
the metric of flat spacetime. But the problem with relativistic
quantum mechanics is that the solutions of the Dirac and
Klein-Gordon equation have instabilities that turn out to
represent the creation
and annihilation of virtual particles from
essentially empty space.
Further understanding led to the development of relativistic
quantum field theory, beginning with quantum
electrodynamics, or QED for
short, pioneered by Feynman, Schwinger and Tomonaga in the
1940s. In quantum field theory, the behaviors and properties of
elementary particles can calculated using a series of diagrams,
called Feynman
diagrams, that properly account for the creation and
annihilation of virtual particles.
The set of the Feynman diagrams for the scattering of two
electrons looks like
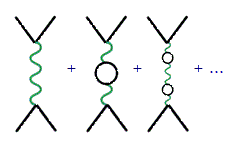
The straight black lines represent electrons.
The green wavy line represents a photon,
or in classical terms, the electromagnetic field between the two
electrons that makes them repel one another. Each small black loop represents
a photon creating an electron and a positron, which then
annihilate one another and produce a photon, in what is called a virtual
process. The full scattering amplitude is the sum
of all contributions from all possible loops of
photons, electrons, positrons, and other available particles.
The quantum loop calculation comes with a very big problem.
In order to properly account for all virtual processes in the
loops, one must integrate over all possible values of momentum,
from zero momentum to infinite momentum. But these loop
integrals for an particle of spin J in D dimensions take the
approximate form
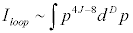
If the quantity 4J + D - 8 is negative, then the integral
behaves fine for infinite momentum (or zero wavelength, by the
de Broglie relation.) If this quantity is zero or positive, then
the integral takes an infinite value, and the whole theory
threatens to make no sense because the calculations just give
infinite answers.
The world that we see has D=4, and the photon has spin J=1.
So for the case of electron-electron scattering, these loop
integrals can still take infinite values. But the integrals go
to infinity very slowly, like the logarithm of momentum, and it
turns out that in this case, the theory can be renormalized so
that the
infinities can be absorbed into a redefinition of a small number
of parameters in the theory, such as the mass and charge
of the electron.
Quantum electrodynamics was a renormalizable theory, and by
the 19402, this was regarded as a solved relativistic quantum
theory. But the other known particle forces -- the weak nuclear
force that makes radioactivity, the strong nuclear force that
hold neurons and protons together, and the gravitational force
that holds us on the earth -- weren't so quickly conquered by
theoretical physics.
In the 1960s, particle physicists reached towards something
called a dual resonance model in an attempt to describe the
strong nuclear force. The dual model was never that successful
at describing particles, but it was understood by 1970 that the
dual models were actually quantum
theories of relativistic vibrating strings and
displayed very intriguing mathematical behavior. Dual models
came to be called string
theory as a
result.
But in 1971, a new type of quantum field theory came on the
scene that explained the weak nuclear force by uniting it with
electromagnetism into electroweak
theory, and it was shown to be renormalizable. Then
similar wisdom was applied to the strong nuclear force to yield quantum
chromodynamics, or QCD,
and this theory was also renormalizable.
Which left one force -- gravity -- that couldn't be turned
into a renormalizable field theory no matter how hard anyone
tried. One big problem was that classical gravitational waves
carry spin J=2, so one should assume that a graviton, the
quantum particle that carries the gravitational force, has spin
J=2. But for J=2, 4 J - 8 + D = D, and so for D=4, the loop
integral for the gravitational force would become infinite like
the fourth power of momentum, as the momentum in the loop became
infinite.
And that was just hard cheese for particle physicists, and
for many years the best people worked on quantum gravity to no
avail.
But the string theory that was once proposed for the strong
interactions contained a massless particle with spin J=2.
In 1974 the question finally was asked: could
string theory be a theory of quantum gravity?
The possible advantage of string theory is that the analog
of a Feynman diagram in string theory is a two-dimensional
smooth surface, and the loop integrals over such a smooth
surface lack the zero-distance, infinite momentum problems of
the integrals over particle loops.
In string theory infinite momentum does not even mean zero
distance, because for strings, the relationship between distance
and momentum is roughly like
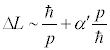
The parameter a' (pronounced
alpha prime) is related to thestring
tension, the fundamental parameter of string theory, by
the relation
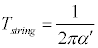
The above relation implies a minimum observable length for a
quantum string theory of
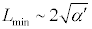
The zero-distance behavior which is so problematic in quantum
field theory becomes irrelevant in string theories, and this
makes string theory very attractive as a theory of quantum
gravity.
If string theory is a theory of quantum gravity, then this
minimum length scale should be at least the size of the Planck
length, which is the length scale made by the combination of
Newton's constant, the speed of light and Planck's constant
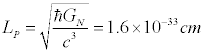
although as we shall see later, the question of length scales in
string theory is complicated by string duality, which can relate
two theories with seemingly different length scales.
Source
عطف به عتف - نگاهی
به پژوهش و ISI در
ایران
امید عمومی - نامه
به ریاست جمهوری
مرز بین ایمان و تجربه
نامه
سرگشاده به حضرت آیت الله هاشمی رفسنجانی
آخرین
مقالات
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
|