نظریه سی پی اچ بر اساس تعمیم سرعت نور از انرژی به ماده بنا شده است.
سی پی اچ در ژورنالها
|
در جست وجوى نقض نسبيت
|
||||||||||||
|
آلن كاستلسكى
«دانشمندان براى آشكار شدن خصوصيات و ساختارهاى احتمالى يك نظريه نهايى در جست وجوى نقض اصول فيزيكى اينشتين هستند كه زمانى مقدس بود.» نسبيت در قلب مهم ترين نظريات بنيادين فيزيك قرار گرفته است. نسبيت آنگونه كه اينشتين آن را در ۱۹0۵ فرمولبندى كرد بر اين ايده كليدى بنا شده كه قوانين فيزيك از نگاه تمام مشاهده گرهاى لخت (اينرسى) (مشاهده گرهايى كه از ديد يك مشاهده گر داراى جهت دلخواه و سرعت ثابت هستند) يكسان است. اين نظريه يك دسته از آثار شناخته شده را پيش بينى مى كند كه از ميان آنها مى توان به ثابت بودن سرعت نور براى تمام مشاهده گرها، كند شدن ساعت هاى در حال حركت، كوتاه شدن طول اجسام متحرك و هم ارزى جرم و انرژى E=mc2 اشاره كرد. آزمايش هاى بسيار دقيق اين نتايج را تائيد مى كنند. نسبيت اكنون يك پايه و ابزار مهم و روزمره براى فيزيكدانان تجربى است: برخورد دهنده هاى ذرات از مزاياى افزايش جرم و طول عمر ذرات پرسرعت به خوبى بهره مى برند و آزمايش با ايزوتوپ هاى راديواكتيو نشان دهنده تبديل جرم به انرژى است. حتى كاربران و بهره برداران دستگاه هاى الكترونيك نيز تحت تاثير اين پديده ها هستند. در سيستم مكان يابى جهانى بايد تصحيح مربوط به تاخير زمانى را در نظر گرفت. اين تاخير زمانى سرعت كار ساعت هاى موجود در مدارهاى ماهواره اى را تغيير مى دهد. با اين حال در سال هاى اخير تلاش براى يكى كردن نيروها و ذرات شناخته شده در يك نظريه نهايى براى عده اى از فيزيكدانان اين انگيزه را به وجود آورده كه درباره امكان تقريبى بودن اصول نسبيت تحقيق كنند. اين انتظار وجود دارد كه مشاهده انحرافى كوچك از نظريه نسبيت طليعه نخستين آزمايش ها براى جست وجو و تحقيق درباره يك نظريه نهايى است. ثابت بودن يا ناوردايى؛ قوانين فيزيك براى مشاهده گرهاى مختلف نشان دهنده تقارن در فضا و زمان (فضا _ زمان) است كه تقارن لورنتس ناميده مى شود. هنريش آنتوان لورنتس فيزيكدان هلندى است كه براى نخستين بار در دهه ۱۸۹۰ در اين باره تحقيق كرده است. كره كامل نمايش دهنده تقارنى است كه به عنوان تقارن تحت دوران (چرخش) شناخته مى شود: كره را در هر جهت و به هر ميزان بچرخانيد كاملاً مشابه به نظر مى رسد. تقارن لورنتس اينگونه بر روى تشابه اشيا بنا نشده است بلكه مبناى آن يكى بودن قوانين فيزيك تحت تبديلات دورانى و بوست (boost كه سرعت را تغيير مى دهد) است. مشاهده گرهاى لخت مستقل از اينكه داراى چه جهت و چه سرعت ثابتى هستند قوانين فيزيك را يكى مى بينند. هنگامى كه تقارن لورنتس درنظر گرفته شود فضا- زمان همسانگرد به نظر مى رسد، بدين معنى كه همه جهت ها و حركت هاى ثابت هم ارز هستند و هيچ كدام بر ديگرى برترى ندارند. تقارن فضا _ زمان لورنتس هسته اصلى نظريه نسبيت را تشكيل مى دهد. با دانستن قواعد تبديلات لورنتس مى توان تمام پيش بينى هاى شناخته شده نسبيت را به دست آورد. تا قبل از مقاله ۱۹۰۵ اينشتين، معادلات مربوط به اين پديده ها توسط محققان ديگرى از جمله خود لورنتس به دست آمده بود. اما آنها اين معادلات را به عنوان تغييرات فيزيكى در اشيا تعبير مى كردند؛ به عنوان مثال طول پيوند بين اتم ها كوتاه مى شود تا موجب ايجاد پديده انقباض طول شود. سهم بزرگ اينشتين اين بود كه او تمام قطعات را به هم پيوند داد و آشكار ساخت كه طول ها و آهنگ كار ساعت ها ارتباط تنگاتنگى با يكديگر دارند و بدين ترتيب تصور فضا و زمان در مفهوم جديدى به نام فضا- زمان يكى گشتند. تقارن لورنتس يك عنصر كليدى و پايه بهترين توصيفات ما از ذرات بنيادى و نيروها است. تقارن لورنتس هنگامى كه با اصول مكانيك كوانتومى تركيب مى شود چارچوبى را بنا مى كند كه نظريه ميدان هاى كوانتومى نسبيتى ناميده مى شود. در اين چارچوب هر ذره و نيرو توسط ميدانى توصيف مى شود كه تمام فضا- زمان را پر كرده و داراى تقارن لورنتس است. ذراتى مانند الكترون ها و فوتون ها به عنوان برانگيختگى هاى موضعى كوانتوم هاى ميدان مربوطه شناخته مى شوند. مدل استاندارد ذرات كه تمام ذرات و نيروهاى غيرگرانشى شناخته شده (شامل الكترومغناطيس؛ برهمكنش ضعيف و برهمكنش قوى) را توضيح مى دهد يك نظريه ميدان كوانتومى نسبيتى است. لزوم برقرار بودن تقارن لورنتس به شدت نوع برهمكنش و طرز رفتار اين ميدان ها را مقيد و مشخص مى سازد.
بسيارى از برهمكنش ها كه مى توانند به صورت جملات محتمل در معادلات اين نظريه ظاهر شوند به دليل نقض تقارن لورنتس ممنوع است.
مدل استاندارد شامل برهمكنش گرانشى
نيست. بهترين توصيف ما از گرانش يعنى نظريه نسبيت عام اينشتين نيز
از تقارن لورنتس تبعيت مى كند. (كلمه «عام» يعنى شامل گرانش است.
گرانش در نسبيت «خاص» در نظر گرفته نمى شود.) در نسبيت عام، مانند
قبل، قوانين فيزيك در يك مكان از ديد مشاهده گرهايى كه داراى جهت هاى
مختلف و سرعت هاى متفاوت هستند يكسان است. اما وجود گرانش مى تواند
مقايسه پيچيده اى بين آزمايش ها در دو مكان متفاوت ايجاد كند.
نسبيت عام يك نظريه كلاسيك غيركوانتومى) است و كسى نمى داند كه
چگونه مى توان آن را به صورت رضايت بخشى با مدل استاندارد تركيب
كرد.
• وحدت نيروها و مقياس پلانك اين تركيب مدل استاندارد و نسبيت عام به طور حيرت انگيزى در توصيف طبيعت موفق است. در آن تمامى پديده هاى بنيادى شناخته شده و نتايج آزمايشگاهى به خوبى توضيح داده مى شود و هيچ گونه شواهد آزمايشگاهى كشف شده فراتر از آن موجود نيست. با اين حال بسيارى از فيزيكدانان مى پندارند كه اين تركيب رضايت بخش نيست. يك پايه اين دشوارى ها اين است كه هر چند دو نظريه داراى فرمول بندى درخشانى هستند اما در اين شكل خود، از ديدگاه رياضى ناسازگارند. در شرايطى مانند آزمايش كلاسيك حركت نوترون هاى سرد برخلاف ميدان گرانشى زمين كه بايد هم گرانش را در نظر گرفت و هم فيزيك كوانتومى را، نيروى گرانشى به عنوان يك نيروى خارجى به توصيف كوانتومى اضافه مى شود. اين مدل هاى ساخته شده ممكن است كه از ديد آزمايشگاهى كارآمد باشند. اما نمى توان آنها را به عنوان يك توصيف بنيادين، سازگار و رضايت بخش درنظر گرفت. اين مورد مانند آن است كه حمل يك شىء توسط فرد را مى توان با درنظر گرفتن نيروهاى وارد بر استخوان ها و اندام هاى بدن و در سطح مولكولى با دقت زيادى توضيح داد و يا مى توان ماهيچه ها را به عنوان جعبه هاى بسته اى درنظر گرفت كه قادر به فراهم كردن نيروهاى خاص در محدوده هاى مشخص هستند. به اين دليل و همچنين دلايل ديگر، بسيارى از فيزيكدانان معتقدند كه فرمول بندى يك نظريه نهايى امكان پذير است (توصيفى كامل و واحد از طبيعت كه در آن گرانش و فيزيك كوانتوم با هم تركيب شده اند.) يكى از نخستين فيزيكدانانى كه بر روى ايده نظريه واحد كار كرد خود اينشتين بود كه سال هاى آخر عمر خود را صرف اين مسئله كرد. هدف او دست يافتن به نظريه اى بود كه نه تنها گرانش بلكه الكترومغناطيس را نيز دربرگيرد. از بخت بد، او بسيار زود با اين مسئله درگير شده بود. هم اكنون ما معتقديم كه الكترومغناطيس رابطه نزديكى با نيروهاى ضعيف و قوى دارد. (نيروى قوى بين كوارك ها عمل مى كند كه سازنده ذراتى مانند پروتون و نوترون هستند، در حالى كه نيروى ضعيف عامل فعاليت هاى راديواكتيو و همچنين واپاشى نوترونى است.) تنها پس از يافته هاى آزمايشگاهى بعد از مرگ اينشتين بود كه نيروهاى قوى و ضعيف به طور جداگانه و بدون تركيب با الكترومغناطيس و گرانش به خوبى فرمول بندى و درك شدند. يك رهيافت فراگير و اميدبخش به چنين نظريه نهايى، نظريه ريسمان است. اين نظريه بر اين ايده بنا شده كه تمام ذرات و نيروها را مى توان براساس اشيايى يك بعدى («ريسمان ها») به همراه رويه هاى دوبعدى و بالاتر كه به آنها ابررويه مى گويند، توصيف كرد. رهيافت شناخته شده ديگر گرانش كوانتومى حلقه اى loop quantum gravity است كه به دنبال يك تفسير سازگار كوانتومى از نسبيت عام است و پيش بينى مى كند كه فضا از قطعات جداى (كوانتوم ها) حجم و سطح ساخته شده است. شكل نظريه نهايى هرگونه كه باشد اين انتظار وجود دارد كه فيزيك كوانتومى و گرانش در مقياس يك طول بنيادى 10 - 35 m كه به خاطر ماكس پلانك فيزيكدان قرن ۱۹ آلمان طول پلانك ناميده مى شود؛ به طور جداناپذيرى درهم تافته شوند. طول پلانك بسيار كوچك تر از طول هايى است كه مى توان به كمك ميكروسكوپ هاى معمولى ديد و يا در شتاب دهنده هاى انرژى بالا كاويد. بنابراين نه تنها ارائه نظريه نهايى يك چالش جدى است، بلكه انجام مشاهدات مستقيم تجربى براى آزمودن پيش بينى هاى چنين نظريه اى نيز عملاً غيرممكن به نظر مى رسد. با وجود چنين سدهايى باز هم ممكن است راه هايى براى كسب اطلاعات آزمايشگاهى از نظريه نهايى در مقياس پلانك وجود داشته باشد. شايد در آزمايش هايى كه به اندازه كافى حساس هستند، پديده هايى كوچك كه به طور غيرمستقيم بازتابنده فيزيكى جديد در نظريه نهايى است، مشاهده شود. همانند تصاوير روى نمايشگر تلويزيون يا كامپيوتر كه از تعداد زيادى نقاط روشن (Pixle) تشكيل شده اند. اين نقاط در مقايسه با فاصله تماشايى نمايشگر به حدى كوچك است كه تصوير از ديد چشم كاملاً يكنواخت به نظر مى رسد. اما در بعضى شرايط خاص اين نقاط مشاهده مى شوند، به عنوان مثال هنگامى كه گوينده خبر كراواتى راه راه با نوارهاى باريك بپوشد باعث ايجاد طرحى مى شود كه به طرح «موير» معروف است. يكى از چنين طرح هايى كه از طول پلانك نشات مى گيرد نقض نظريه نسبيت است. در فواصل ماكروسكوپيك (معمولى)، فضا- زمان ناورداى لورنتس به نظر مى رسد، ولى ممكن است كه اين تقارن در فواصل به اندازه كافى كوچك به عنوان جلوه اى از وحدت فيزيك كوانتومى و گرانش شكسته شده باشد. انتظار مى رود كه آثار قابل مشاهده نقض نظريه نسبيت در مقياس پلانك در فاصله 10 - 17 to 10 - 34 قرار گرفته باشند. براى درك بهتر اين ابعاد بايد در نظر آوريد كه قطر تار موى انسان 10 30 برابر ابعاد كيهان است در حالى كه 10 - 17 نسبت به قطر مو مانند قطر موى انسان به قطر مدار نپتون است. بنابراين مشاهده نقض نسبيت به آزمايش هايى بسيار حساس تر از آنچه تاكنون انجام شده احتياج دارد. تقارن بنيادين ديگرى از فضا- زمان كه مى تواند نقض شودCPT نام دارد. اين تقارن هنگامى وجود دارد كه قوانين فيزيك تحت سه تبديل زير (به طور همزمان) تغيير نكنند: تعويض ذره و پادذره مزدوج بار، C بازتاب در آينه (تبديل پاريته، P و برگشت زمانى (T) . مدل استاندارد از تقارن CPT تبعيت مى كند، در حالى كه اين تقارن ممكن است در نظريه هايى كه نسبيت را نقض مى كنند، شكسته شده باشد.
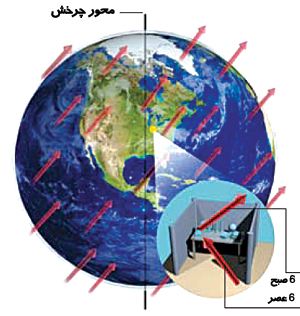
چرخش زمين يك آ زمايشگاه را نسبت به ميدان بردارى نقض كننده نسبيت (پيكان ها) مى چرخاند. از ديد چارچوب آزمايشگاه جهت ميدان بردارى در طول روز تغيير مى كند، كه با استفاده از آن مى توان نقض نسبيت را مشاهده كرد. به عنوان مثال ممكن است نسبت جرم دو جسم غيرهمجنس در طول روز متغير باشد.
•نقض خودبه خود نقض نسبيت در يك نظريه نهايى چگونه خود را نشان مى دهد؟ يك روش طبيعى و زيبا شكست خودبه خود تقارن لورنتس است. اين مورد بايد كاملاً مشابه شكست خودبه خود تقارن در موارد ديگر باشد هنگامى اتفاق مى افتد كه قوانين پايه متقارن هستند در حالى كه سيستم هاى واقعى اين گونه نيستند. براى درك ايده عمومى شكست خودبه خود تقارن يك ميله باريك استوانه اى را كه به صورت عمودى بر روى يك سطح صاف قرار گرفته در نظر بگيريد. تصور كنيد يك نيروى عمودى به سمت پايين بر روى ميله وارد مى گردد. اين سيستم به طور كامل تحت دوران حول محور ميله متقارن است: ميله استوانه اى است و نيرو به صورت عمودى وارد مى شود، بنابراين قوانين و معادلات فيزيكى در اين شرايط تحت دوران ناوردا هستند. اما اگر نيرو به اندازه كافى زياد شود ميله در يك جهت خم مى گردد كه تقارن تحت دوران را به صورت خودبه خود مى شكند. در مورد نقض نسبيت، معادلات توصيف كننده ميله و نيرو با معادلات نظريه نهايى جايگزين مى شوند. به جاى ميله ميدان هاى كوانتومى مواد و نيروها قرار مى گيرند. در اغلب موارد اندازه ميدان پس زمينه اى طبيعى چنين ميدان هايى صفر است. با اين حال در بعضى شرايط ميدان هاى پس زمينه مقادير غيرصفرى كسب مى كنند. تصور كنيد چنين حالتى براى ميدان الكتريكى رخ دهد. از آنجا كه ميدان الكتريكى داراى جهت است (بردار)، هر مكانى در فضا داراى جهت ويژه اى مى شود كه توسط جهت ميدان الكتريكى در آن مكان تعيين مى شود. يك بار الكتريكى نقطه اى در آن جهت شتاب مى گيرد. در نتيجه تقارن دورانى (و همچنين تقارن «بوست») مى شكند. چنين نتايجى براى يك ميدان تانسورى غيرصفر نيز برقرار است (بردارها حالت خاص تانسورها هستند. چنين ميدان هاى تانسورى غيرصفرى در مدل استاندارد به وجود نمى آيند، اما بعضى از نظريه هاى بنيادى مانند نظريه ريسمان شامل جنبه هايى هستند كه مناسب شكست خودبه خود تقارن لورنتس هستند. اين ايده كه شكست خودبه خود تقارن لورنتس و مشاهده نقض نظريه نسبيت مى تواند در نظريه ريسمان و تئورى هاى ميدان شامل گرانش اتفاق افتد نخستين بار توسط من و استوارت ساموئل از كالج نيويورك در سال ۱۹۸۹ پيشنهاد شد. من و روبرتوس پوتينگ در سال ۱۹۹۱ اين موضوع را به شكست تقارن CPT در نظريه ريسمان گسترش داديم. بعد از آن روش هاى متعددى براى نقض نظريه نسبيت در نظريه ريسمان و ديگر رهيافت هاى گرانش كوانتومى پيشنهاد شد. اگر شكست تقارن لورنتس واقعاً جزيى از نظريه نهايى باشد، مشاهده نقض نسبيت نخستين مشاهدات آزمايشگاهى را براى چنين نظريه اى فراهم خواهد كرد.
تعميم مدل استاندارد فرض كنيد نظريه بنيادى طبيعت از طريق مكانيسم هايى شكست تقارن لورنتس يا CPT را شامل مى شود. اكنون اين پرسش پيش مى آيد كه اين نقض ها چگونه خود را در آزمايش نشان مى دهند و نسبت آنها با فيزيك امروزى به چه صورت است؟ براى پاسخ به اين پرسش به يك چارچوب نظرى كلى احتياج داريم كه بتواند تمام پديده هايى را كه ممكن است در آزمايشگاه رخ دهد، دربرگيرد. به كمك چنين چارچوبى مى توان پارامترهاى آزمايشگاهى را محاسبه، آزمايش هاى مختلف را مقايسه و پديده هاى قابل انتظار را پيش بينى كرد. براى ساخت چنين چارچوبى بايد به اصول طبيعى و بدون شك زير پايبند بود. اول آنكه تمام پديده هاى فيزيكى مستقل از دستگاه مختصاتى هستند كه براى توصيف فضا- زمان انتخاب مى كنيم. دوم آنكه آزمايش هاى موفق مدل استاندارد و نظريه نسبيت عام نشان مى دهند كه نقض تقارن لورنتس و CPT بايد اثر بسيار كوچكى داشته باشند. پيروى از اين معيارها و به كار بردن نيروها و ذرات شناخته شده ما را بر مجموعه اى از جملات ممكن _ برهمكنش هاى ممكن _ رهنمون مى شود كه مى توان آنها را به معادلات نظريه اضافه كرد. هر كدام از اين جملات معادل يك ميدان تانسورى با مقدار پس زمينه اى غيرصفر است. ضرايبى كه دامنه آنها را مشخص مى كنند، نامعلوم هستند كه البته بسيارى از آنها ممكن است در يك نظريه نهايى مشخص صفر باشند.نتيجه نهايى نظريه اى است كه به آن تعميم مدل استاندارد (SME = standard Model Extention) مى گويند. زيبايى اين فرمول بندى در عموميت آن است: هر گونه منشاء دلخواه فيزيكى يا فلسفى كه براى نقض نسبيت در نظر بگيريد و همچنين نتايج آن در طبيعت بايد به كمك SME قابل توضيح باشد زيرا اين نظريه تمام اصلاحات و تعميم هاى ممكن نسبيت را كه با مدل استاندارد سازگار است، دربرمى گيرد. براى مجسم كردن آثار شكست تقارن لورنتس، مفيد است كه فرض كنيم فضا- زمان داراى يك جهت ذاتى است. در مواردى كه يك ميدان بردارى به عنوان يك جمله ويژه در معادلات SME ظاهر مى شود اين جهت ذاتى فضا- زمان بر جهت اين ميدان بردارى منطبق است. براى ميدان هاى تانسورى نيز موضوع مشابه ولى كمى پيچيده تر است. حركت و برهمكنش ذرات به دليل وجود چنين ميدان هاى پس زمينه اى، وابستگى جهت دارى به خود مى گيرد مانند حركت ذره باردار در ميدان الكتريكى يا مغناطيسى. چنين پديده هايى در مورد نقض CPT نيز اتفاق مى افتد، اما اين مورد به علت تفاوت كوپلاژ ذره و ضدذره با ميدان پس زمينه است. SME پيش بينى مى كند كه رفتار ذرات مى تواند به روش هاى گوناگونى تحت تاثير نقض نسبيت قرار گيرد خصوصيات ذرات و برهمكنش آنها به جهت حركت (نقض تقارن دورانى) و سرعت آنها (نقض تقارن «بوست») بستگى دارد. ذره ممكن است داراى اسپين باشد (كميت نشان دهنده اندازه حركت زاويه اى درونى)، در اين حالت رفتار ناشى از نقض نسبيت مى تواند به جهت و اندازه اسپين وابسته باشد. يك ذره مى تواند تصوير آيينه اى پادذره خود نباشد (نقض CPT) نوع رفتار مى تواند به نوع ذره بستگى داشته باشد؛ به عنوان مثال شايد پروتون بيش از نوترون تحت تاثير قرار بگيرد. اين پديده ها ردهاى زيادى از خود به جا مى گذارند كه مى توان در آزمايش ها به دنبال آنها گشت. تعدادى از اين آزمايش ها از هم اكنون آغاز شده اند، اما هنوز هيچ كدام شواهد متقنى در رد نظريه نسبيت به دست نداده اند.
تقارن فضا- زمان نسبيت رعايت مى شود تقارن لورنتس يكى از خصوصيات بنيادى جهان بيرونى است كه اهميت زيادى براى فيزيك دارد. اين تقارن داراى دو جزء است: تقارن دورانى و تقارن بوست. تصور كنيد دو ميله و دو ساعت داريم كه ميله ها از دو ماده متفاوت ساخته شده اند ولى هنگامى كه پهلو به پهلوى يكديگر قرار مى گيرند طول يكسانى را نشان مى دهند و ساعت ها نيز به روش هاى متفاوتى كار مى كنند ولى همزمان هستند. (a). تقارن دورانى برقرار است اگر يك ميله و يك ساعت را نسبت به ديگرى بچرخانيم طول ميله ها نسبت به يكديگر تغيير نكرده و همزمانى ساعت ها نيز به هم نخورد (b). تقارن بوست شامل آن چيزى است كه هنگام حركت يك ميله به همراه يك ساعت با سرعت ثابت نسبت به ميله و ساعت ثابت اتفاق مى افتد. تقارن بوست پيش بينى مى كند كه طول ميله در حال حركت از ديد ناظر ساكن كوتاه تر شده و ساعت همراه آن نيز كندتر كار مى كند (C) . هنگامى كه فضا و زمان تركيب شده و تشكيل فضا- زمان را مى دهند شكل فرمول بندى رياضى تقارن بوست بسيار شبيه تقارن دورانى خواهد بود. يك تقارن وابسته به تقارن لورنتس تقارن CPT است كه بيانگر تغيير علامت بار الكتريكى، تغيير جهت پاريته (معكوس آينه اى نسبت به يك نقطه) و برگردان زمانى هستند. اين تقارن پيش بينى مى كند كه اگر يك ساعت با معادل پادماده اى خودش جايگزين شود (تغيير علامت بار) همچنين سر و ته شود (معكوس آينه اى _ پاريته) و در جهت معكوس زمانى كار بكند، آنگاه همان زمان را نشان خواهد داد كه ساعت اول نمايش مى دهد. (d).
محاسبات رياضى نشان مى دهد كه در نظريه ميدان هاى كوانتومى هرگاه
تقارن لورنتس در نظر گرفته شود، تقارن CPT نيز برقرار خواهد بود.
نسبيت نقض مى شود شكست تقارن لورنتس را مى توان به وسيله يك ميدان بردارى حاضر در فضا- زمان نمايش داد. ذرات و نيروها با اين ميدان (پيكان ها) برهمكنش مى كنند، همانگونه كه يك ذره باردار با ميدان الكتريكى (كه يك ميدان بردارى است) برهمكنش مى كند. در نتيجه برخلاف زمانى كه تقارن لورنتس برقرار است تمام جهت ها و سرعت ها هم ارز نيستند. دو ميله غيريكسان كه در يك جهت نسبت به ميدان بردارى داراى طول يكسان هستند (شكل سمت چپ) ممكن است در جهت ديگر هم طول نباشد (شكل وسط) مشابه آن دو ساعت كه در يك جهت هم زمان هستند ممكن است در جهت ديگر همزمانى شان را از دست بدهند. به علاوه دو ساعت و دو ميله غيريكسان در هنگام حركت ممكن است اتساع زمانى و انقباض طولى متفاوتى را بسته به جنس و جهت حركتشان نشان دهند. (شكل راست)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
|
Sub quantum space and interactions from photon to fermions and bosons |
|
نامه سرگشاده به حضرت آیت الله هاشمی رفسنجانی |
آرشیو موضوعی

از آغاز کودکی به پدیده های فیزیکی و قوانین حاکم بر جهان هستی کنجکاو بودم. از همان زمان دو کمیت زمان و انرژی بیش از همه برایم مبهم بود. می خواستم بدانم ماهیت زمان چیست و ماهیت انرژی چیست؟