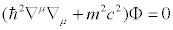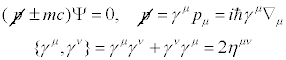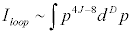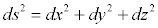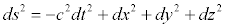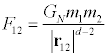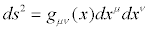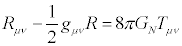CPH Theory نظریه سی پی اچ

فیزیکدانان که هنوز از موفقیت تئوری الکتروضعیف دچار گیجی بودند، توجه خود را به حل نیروی قوی معطوف نمودند. منشا تئوری واکنش قوی به سال 1935 برمی‌گردد وقتی که فیزیکدان ژاپنی «هیدکی یوکاوا» پیشنهاد داد که پروتونها و نوترونها توسط یک نیروی جدید که توسط مبادله ذراتی به نام «پی مزون» خلق می‌شود در هسته اتم با یکدیگر نگه داشته می‌شوند.

در دهه‌های 1950 و 1960 فیزیکدانان از شکننده‌های اتم در آزمایشگاه‌ها موفق به کشف صدها نوع از ذرات واکنش قوی که «هادرون»ها نامیده می‌شوند شدند(که شامل هم مزون و هم دیگر ذرات واکنش قوی مانند پروتون و نوترون می‌باشند.هیچکس نمی‌توانست بیان نماید چرا دنیایی که تا دهه 1930 بوضوح ساده بنظر می‌رسید به یکباره اینچنین پیچیده شد. زمانی تصور می‌شد که کل کائنات از چهار ذره و دو نیرو (الکترون، پروتون، نوترون، نوترینو، نور و گرانش) ساخته شده، اما فیزیکدانان با سیلی از هادرون‌های جدید که در آزمایشگاهها کشف شدند مواجه گردیدند. یک تئوری جدید نیاز بود تا به این هرج و مرج سر و سامان بدهد. در آن زمان «اپنهایمر» به شوخی گفت که "جایزه نوبل باید به فیزیکدانی داده شود که امسال یک ذره جدیدی را کشف نکرده باشد". تا سال 1984 بیش از دویست ذره جدید کشف شد.

فیزیکدانان همانند «مندلیف» که تقریبا در یک قرن پیش قانون‌مندی عناصر طبیعت و تنظیم آنها در «جدول مندلیف» را انجام داد، شروع به جستجو برای تقارنی کردند که با آن بتوان همه هادرون‌ها را طبقه‌بندی کرد. در اوایل دهه 1960 «گل‌مان» نشان داد که می‌توان هادرون‌ها را در یک الگوی هشت‌تائی گروه‌بندی کرد. او همانند مندلیف توانست وجود و حتی خواص ذراتی را که تا آن زمان کشف نشده بودند، پیش‌گویی کند. اما اگر این الگو، قابل مقایسه با جدول مندلیف بود، در آن چه چیزهایی جای الکترون‌ها و پروتون‌ها را می‌توانستند بگیرند؟
بعدها کشف شد که این الگو به خاطر وجود ذرات زیرهسته‌ای که به آنها لقب کوارک دادند، بوجود می‌آید. در حقیقت با ترکیب سه نوع کوارک می‌توانستند تمام ذراتی که در آزمایشگاهها تولید می‌شدند را توصیف کنند.

در کل شش نوع کوارک وجود دارد که دو تا دو تا شناخته می‌شوند:

بار الکتریکی کوارکها به صورت کسری می‌باشد، مثلا 3/1 و 3/2 ، هادرونها ازکوارکها تشکیل شده اند اگر چه کوارکها دارای بارهای الکتریکی کسری میباشند ولی هادرونی که از ترکیب آنها بدست میاید دارای بار الکتریکی صحیح ایست. کوارکها علاوه بر بار الکتریکی حامل یک نوع بار دیگر به نام «بار رنگی» نیز می‌باشند. نیروی مابین ذرات دارای بار رنگی خیلی قوی است ؛ به همین دلیل است که این نیرو نیروی قوی نامیده میگردد. ذرات حامل این نیروی قوی که بین کوارکها رد و بدل می‌شود، «گلئون»ها نام دارند. بار رنگی نسبت به بارالکترومغناطیسی دارای ماهیت متفاوتی است، گلوئون‌ها خودشان نیز دارای بار رنگی هستند که این امر موجب شگفتی بیشتر آنها می‌گردد زیرا برعکس فوتونها که ذرات حامل نیروی الکترومغناطیسی هستند می‌باشند، فوتونها با وجود اینکه حامل نیروی الکترومغناطیسی هستند ولی خودشان فاقد بارالکتریکی می‌باشند. از طرفی هادرون‌ها که از کوارکها تشکیل می‌شوند فاقد بار رنگی می‌باشند و از نظر بار رنگی خنثی هستند، به همین دلیل است که ما اثرات این نیروی قوی را فقط در بین هادرونها می‌بینیم. تئوری‌ای که این نیرو را توضیح میداد، «کرومودینامیک کوانتوم» نام داشت.
در سال 1974 ، «شلدون گلاشو» و «هوارد جرجی» تئوری‌ای پیشنهاد کردند که طی آن نیروی قوی با الکتروضعیف متحد می‌شد و آنرا «تئوری وحدت بزرگ» (گات) نامیدند. این تئوری پیشگویی می‌کند که کوارک می‌تواند تبدیل به الکترون شود. این همچنین بدان معنا است که پروتون میتواند به الکترون تبدیل شود. زیرا پروتون از سه کوارک تشکیل شده است. هرچند تئوری گات پیشرفتی قابل توجه را در اتحاد نیروی الکتروضعیف با نیروی قوی عرضه می‌کرد ولی از لحاظ تئوری همچنان ناقص بود. بطور مثال این تئوری نمیتواند بیان کند که چرا سه کپی فامیل‌های ذرات (خانواده‌های الکترون، میون و تائو) وجود دارند. بعلاوه ثابتهای قراردادی زیادی در تئوری وجود داشت.

علیرغم مشکلات تئوری گات، فیزیکدانان هنوز معتقد بودند که ممکن است تئوری‌ای برای وحدت گرانش وجود داشته باشد.

در 1971 یک تئوری جدید میدان کوانتوم وارد صحنه شد که می‌توانست نیروی هسته‌ای ضعیف و الکترومغناطیس را با هم متحد کند. برای اولین بار از زمان ماکسول یعنی تقریبا صد سال، نیروهای طبیعت قدمی دیگر به طرف وحدت برداشتند. یکبار دیگر اسرار معما تقارن مقیاس بود.
واکنشهای ضعیف مربوط به رفتار الکترونها و شرکای آنها بنام نوترینوها می‌باشد. از تمام ذرات کائنات، نوترینو شاید نادرترین آنها باشد، زیرا شدیدا فرّار می‌باشد. نوترینو، بار و احتمالا جرم ندارد و بسیار بسیار سخت آشکار می‌باشد.
در سال 1933 فیزیکدان بزرگ ایتالیایی انریکو فرمی، اولین تئوری جامع از این ذرات فرّار که نوترینو (ذرات کوچک خنثی به زبان ایتالیایی) نامید، به طبع رساند.
تجارب در ارتباط با نوترینوها بسیار مشکل بود زیرا نوترینوها خیلی نافذند و از حضورشان هیچ ردی به جا نمی‌گذارند. در حقیقت آنها می‌توانند بسهولت به داخل کره زمین رخنه نمایند و از طرف دیگر زمین خارج شوند. در واقع اگر تمام منظومه شمسی پر از سرب سخت بود، بعضی از نوترینوها قادر بودند حتی به آن حصار مستحکم نیز رخنه نمایند.
وجود نوترینو نهایتا در سال 1953 در یک تجربه بسیار مشکل در حین مطالعه تشعشعات فراوان خلق شده توسط رآکتور هسته‌ای تائید شد.
از زمان کشف، سالها مخترعین سعی نمودند تا به استفاده‌های عملی نوترینو فکر نمایند. بیشتر این افراد جسور مایل بودند تا یک «تلسکوپ نوترینو» بسازند. با این تلسکوپ ما می‌توانیم مستقیما در داخل صدها کیلومتر صخره‌های سخت جستجو کنیم، هر کس اهدافی نظیر این برای تلسکوپ پیش‌بینی می‌کرد. ایده تلسکوپ نوترینو مسلما بسیار خوب است، اما یک مانع وجود دارد: از کجا ما می‌توانیم فیلم عکاسی پیدا نمائیم که بتواند نوترینو را متوقف کند؟ هر ذره‌ای که بتواند به تریلیونها تن صخره رسوخ نماید براحتی می‌تواند به فیلم عکاسی هم نفوذ کند.
پیشنهاد دیگر خلق یک «بمب نوترینو» بود.فیزیکدان هانیز پاجلز می‌نویسد که این یک اسلحه مطلوب صلح‌طلب می‌باشد. مانند یک بمب که می‌توند براحتی جانشین بمب هسته‌ای مرسوم باشد؛ این بمب با سر و صدا منفجر شده و منطقه مورد هدف را با سیلی عظیم از نوترینو‌ها بمباران می‌کند، بعد از اینکه همه را ترساند، نوترینوها بدون هیچ صدمه‌ای از میان همه چیز عبور می‌کنند.
علاوه بر نوترینو، اسرار واکنشهای ضعیف با کشف ذرات جدید مانند میون، عمیقتر شد. قبلا در سال 1937 وقتی که این ذره در عکسبرداری اشعه کیهانی کشف شد، بنظر درست شبیه الکترون می‌آمد اما بیش از دویست بار سنگین‌تر از آن بود. برای تمام مقاصد آن ذره درست یک الکترون سنگین بود. فیزیکدانان در سال 1962 با استفاده از شکافنده اتم نشان دادند که میون همچنین شریک مجزای خودش، نوترینوی میون را دارد. در سال 1978 بار دیگر یک جفت برای الکترون کشف شد ولی اینبار سه‌هزار و پانصد بار سنگین‌تر بود و «تائو» نام گرفت با شریک مجزای خودش بنام نوترینوی تائو فیزیکدانان حدس زدند که نیروی بین الکترونها و نوترونها توسط تبادل یکسری جدید ذرات به نام ذرات W به جای Weak ایجاد می‌شود.

در اینجا هم تئوری درست با دیاگرامهایی شبیه دیاگرامهای فاینمن قابل توصیف بود، به جای جفت الکترون-پوزیترون، کافیست که الکترون-نوترینو را جایگزین کنیم و به جای فوتونها ، ذرات دبلیو بگذاریم. مشکل اینجا بود که تئوری با استفاده از تقارن مقیاس قابل بهنجارش نبود و تئوری با بینهایت‌ها درگیر بود. تا سالها فیزیکدانان درگیر آن بودند. تئوری یانگ-مایلز محتوی یک تقارن ریاضی جدید بود که به «واینبرگ» و «سالم» اجازه داد تا نیروهای ضعیف و الکترومغناطیس را به همان وضع با هم متحد کنند.
فیزیکدانها بطور قوی باور کرده بودند که نیروهای ضعیف بصورت نزدیکی به نیروهای الکترومغناطیسی مربوط هستند، سرانجام آنها کشف کردند که در فواصل بسیارکوتاه ( درحدود 10 به قوه 18- متر ) قدرت برهمکنش ضعیف قابل برابری با برهمکنش الکترومغناطیسی است، به عبارت دیگر در سی برابر آن فاصله قدرت برهمکنش ضعیف يك ده‌هزارم ( سه برابر ده به توان منفي هفده) برهمکنش الکترومغناطیسی است، درفواصل مثلا برای کوارکهای داخل یک پروتون یا نوترون ( ده به قوه منفي پانزده ) ، نیرو حتی از آنهم ضعیف‌تر است.
فیزیکدانها نتیجه گرفته اند که درحقیقت نیروهای الکترومغناطیسی و ضعیف اساسا قدرتهای یکسانی دارند , این به این دلیل است که قدرت برهمکنش به طور قوی به دوعامل جرم ذرات حامل نیرو و فاصله برهمکنش بستگی دارد ، تفاوت مابین قدرتهای مشاهده شده آنها از تفاوت بزرگ در جرم ذرات W و Z که بسیار پرجرم هستند و فوتونها که تا آنجا که ما می دانیم فاقد جرم هستند ناشی می گردد.

به مجرد اینکه نسبیت خاص بر پایه‌های تئوری و مشاهدات استوار شد ، فیزیکدانان دریافتند که معادله شرودینگر در مکانیک کوانتومی تحت تبدیلات لورنتس ناوردا نیست. بنابراین مکانیک کوانتومی که با موفقیت در دهه 1920 توسعه داده شده بود ، درباره توصیف رفتار ذراتی که نزدیک به سرعت نور حرکت می‌کردند پاسخگو نبود.
مشکل آنجا بود که معادله شرودینگر نسبت به زمان از درجه اول و نسبت به مختصات فضایی از درجه دو بود. معادله کلین-گوردون نسبت به هر دو آنها یعنی فضا و زمان از درجه دو بود و راه‌ حلی برای ذرات با اسپین صفر بود.

دیراک ریشه دوم معادله کلین-گوردون را با استفاده از ماتریسی به نام "ماتریس گاما" بوجود آورد و راه حلی شد برای ذرات با اسپین ½

اما مشکل مکانیک کوانتومی نسبیتی آن بود که معادلات دیراک و کلین-گوردون در تفسیر تولید و نابودی ذرات از فضای تهی ، خلا ، ناتوان بودند.
یافته‌های بیشتر با "الکترودینامیک کوانتوم" آغاز شد که بوسیله فاینمن، شرودینگر و توموناگا در دهه 1940 پایه‌گذاری شد
در تئوری میدان کوانتوم رفتار و خواص ذرات بنیادین توسط یک‌ سری دیاگرامها به نام دیاگرامهای فاینمن قابل محاسبه هستند که به دقت تولید و نابودی ذرات را شرح می‌دهند. مجموعه دیاگرامهای فاینمن برای تفرق دو الکترون به مانند شکل زیر است.

خطهای راست سیاه نمایانگر الکترونها هستند و خطهای موجی سبز نمایانگر فوتون و هر حلقه نشاندهنده تولید یک الکترون و پوزیترون از یک فوتون می‌باشد که یکدیگر را نابود می‌کنند و یک فوتون خلق می‌کنند. محاسبه کامل دامنه تفرق، جمع روی همه حالتهای ممکن برای فوتونها، الکترونها، پوزیترونها و سایر ذرات بود.
محاسبات حلقه‌های کوانتومی با یک مشکل بزرگ روبرو بود؛ به منظور محاسبه درست برای فرایند‌ها در حلقه‌ها، باید از یکی روی همه مقادیر تکانه‌های ممکن از صفر تا بینهایت انتگرال گرفته شود، اما این انتگرالها برای یک ذره با اسپین j در D بعد تقریبا به شکل زیر بود:

اگر مقدار 4j+D-8 " منفی باشد، انتگرال برای تکانه بینهایت (یا طول موج صفر، بر اساس فرمول دوبروی) خوش رفتار خواهد بود. اگر این طول مقدار صفر یا مثبت باشد، جواب انتگرال بینهایت میشود و نظریه‌ای که درست می‌نمود به نظر غیرقابل درک می‌رسید چون فقط جوابهای بینهایت به ما می‌داد.
جهانی که ما می‌بینیم چهار بعد دارد و یک فوتون اسپین 1 دارد، پس در مورد تفرق الکترون-الکترون این انتگرال همچنان جواب بینهایت‌می‌داد، اما جواب انتگرال به کندی به سمت بینهایت میل می‌کرد و در این مورد به نظر می‌رسید که تئوری می‌تواند بهنجارش شود به صورتی که بینهایت‌ها به تعداد کمی پارامتر تبدیل می‌شوند، مانند جرم و بار الکترون.
الکترودینامیک یک تئوری است که دو پارامتر دارد، بار و جرم الکترون. معادلات ماکسول علاوه بر نسبیت خاص، تقارن دیگری دارد به نام تقارن مقیاس، که به فاینمن اجازه داد تا سری بزرگی از دیاگرامها را گروه نماید تا پی برد که او می‌تواند براحتی بار و جرم الکترون را برای جذب و از بین بردن بینهایتها دوباره معین نماید.
رویهم رفته این بدان معنا بود که جرم و بار الکترون بطور ضروری جهت شروع، بینهایت فرض می‌شد. ولی آنها بینهایتهایی را که از دیاگرامها پدیدار می‌شدند را محدود می‌کردند و به کلام دیگر قانونمند می‌کردند.
در واقع می‌خواست کاری شبیه به " بینهایت منهای بینهایت مساوی صفر " انجام دهد، و تئوری اوتقریبا به خوبی کار میکرد.
الکترودینامیک کوانتوم یک تئوری قابل بهنجارش بود و در دهه 1940 به عنوان راه حل کوانتوم نسبیتی به آن توجه شد. اما دیگر ذرات شناخته شده که حامل نیروها بودند مانند هسته‌ای ضعیف که باعث رادیواکتیویته بود، هسته‌ای قوی که پروتونها و نوترونها را در هسته در کنار هم نگه می‌داشت و گرانش که ما را روی زمین نگه می‌داشت به این زودی توسط تئوریهای فیزیک تسخیر نشدند.
در دهه 1960 فیزیک ذرات به منظور توصیف نیروی هسته‌ای قوی به مفهومی به نام مدل تشدید دوگانه دست یافت. این مدل هیچگاه در توصیف ذرات آنچنان موفق نبود، ولی در دهه 1970 فهمیده شد که مدل دوگانه در واقع نظریه‌ای کوانتومی برای ریسمانهای مرتعش نسبیتی است و رفتارهای ریاضی عجیبی از خود نشان می‌دهد، در نتیجه مدل دوگانه به عنوان " تئوری ریسمان " نامیده شد.
اما نظریه دیگری که در ابتدای قرن بیستم بوجود آمد ، بار دیگر فیزیکدانان را متعجب ساخت و آن ثابت بودن سرعت نور مستقل از هر ناظری بود. این یک نتیجه مهیج و جالب از آزمایشات " مایکلسون " و " مورلی " بود ؛ اما چگونه می شد آنرا بوسیله فیزیک توجیه کرد. انیشتین با یک نظریه ساده و قدرتمند به نام نسبیت خاص آنرا حل کرد. انیشتین یک هندسه خیالی از سیستم مقیاس بیان کرد . سیستم مقیاس معروفی که اغلب استفاده می شد ، از قانون فیثاغورث پیروی میکردکه در سه بعد به این شکل بود:

این فرمول خاصیت ویژه ای داشت و آن اینکه تحت دوران ناوردا بود. یعنی اینکه طول خط با چرخش در فضا تغییر نمیکرد . در نسبیت خاص این مقیاس بسط داده شد و زمان را نیز شامل شد ، با یک علامت منفی عجیب که فضای چهار بعدی مینکوفسکی نامیده میشود:

درست مانند سیستم فیثاغورث این رابطه هم تحت چرخش ثابت بود. ولی در این رابطه جدید یک چیز جالب دیگر نیز وجود داشت و تحت نوعی چرخش فضا-زمان به نام تبدیلات لورنتس نیز ناوردا بود. و این تبدیلات به ما میگویند که دو ناظر مختلف با سرعتهای ثابت نسبت به یکدیگر ، جهان را چگونه مشاهده میکنند و همچنین به ما می گوید که سرعت نور همیشه ثابت است. انیشتین بعد از آن به سراغ قانون جهانی گرانش نیوتون رفت ؛ در فرمول نیوتون ، نیروی گرانش بین دو جرم m1 , m2 با مجذور فاصله بین آنها رابطه زیر را دارد:

G_N ثابت نیوتون نامیده میشود، میباشد .

قانون نیوتون در تشریح حرکت سیارات به دور خورشید و ماه به دور زمین موفق بود و بسادگی قابل توسعه در تئوری میدان کلاسیک در سیستم های پیوسته بود. اگرچه در آن هیچ توضیحی در مورد تغییر یافتن میدان گرانش در زمان وجود نداشت. بخصوص که مفهوم جدیدی که از نسبیت خاص بدست آمده بود یعنی " هیچ چیزی نمیتواند سریعتر از نور حرکت کند " را نمیتوانست توجیه کند.
انیشتین با یک قدم جسورانه به درکی جدید از شاخه ای از ریاضیات به نام " هندسه نااقلیدوسی " رسید که در آن قانون فیثاغورث تعمیم داده شد تا سیستم مقیاسی که وابسته به فضا-زمان بود را با ضریبی در بر می گرفت:

نیشتین نتیجه گرفت که " برای تدوین قوانین عمومی طبیعت همه دستگاههای مختصات گاوسی اساسا هم ارزند " و آنرا نسبیت عمومی نامید. در این تئوری جدید ، فضا-زمان میتوانست مانند یک توپ خمیده شود. خمیدگی تابعی از g_ab و مشتق اول و دوم آن است . در معادله انیشتین:

خمیدگی فضا-زمان ( که با Rµν و R جایگزین شده ) بوسیله انرژی و تکانه Tµν کل ماده در فضا-زمان مانند سیارات ، ستاره ها غبار بین ستاره ای ، گازها ، سیاه چاله ها و ... تعیین میشود.

منبع: مراکز سازمان ملی پرورش استعدادهای درخشان ایران