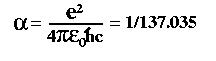نظریه سی پی اچ بر اساس تعمیم سرعت نور از انرژی به ماده بنا شده است.
سی پی اچ در ژورنالها
|
مفهوم و اهمیت عدد 137 در فیزیک
|
|
که در آن به ترتیب e , c , h , e و از چپ به راست بار الکترون، سرعت نور، ثابت پلانک تقسیم بر دو پی و ثابت گذردهی خلاء است در توضیح این عدد گفته شده که زیبایی آن در این است که همه ی ثابت ها که در این رابطه وجود دارند، هرکدام بعد خود را دارد، اما این عدد بی بعد است اهمیت این عدد در آن است که با آن بزرگی کنش الکترومغناطیسی را اندازه می گیرند. این عدد 1/137 با تمام اعداد یک فرق مهم دارد و آن این است که در الکترومغناطیس کوانتومی بطور شگفت انگیزی نقش ایفا می کند هنگامی که می خواهیم یک مرحله ساده را حساب کنیم، مانند هنگامیکه دو الکترون با تبادل یک فوتون از یکدیگر دور می شوند، ما تنها به یک حالت ساده تبادل فوتون نیاز داریم - هر گونه فوتون اضافی با ضریبی از 137/1 منظور خواهد شد
What is the significance of
the number 137 in physics? The
importance of the number 137 is that it is related to the
so-called 'fine-structure constant' of quantum
electrodynamics. This derived quantity is given by combining
several fundamental constants of nature:
where
e is the charge on the electron, c is the speed of light, h-bar
is Planck's constant and the epsilon represents the permittivity
of free space. Despite the fact that each of these constants
have their own dimensions, the fine-structure constant is
completely dimensionless!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
|
Sub quantum space and interactions from photon to fermions and bosons |
|
نامه سرگشاده به حضرت آیت الله هاشمی رفسنجانی |
آرشیو موضوعی

از آغاز کودکی به پدیده های فیزیکی و قوانین حاکم بر جهان هستی کنجکاو بودم. از همان زمان دو کمیت زمان و انرژی بیش از همه برایم مبهم بود. می خواستم بدانم ماهیت زمان چیست و ماهیت انرژی چیست؟