|
مدل جدید کیهانشناسی، توصیف اولین دوره زمانی جهان
را به چالش کشیده است؛ دوره ای که با مدل های جاری قابل دسترسی
نیست.
تورم کیهانی(Cosmological Inflation)، فرضیه ای که
بنابر آن، جهان اولیه یک انبساط بی نهایت سریع را تجربه می کند، یک
الگوی مورد پسند در کیهانشناسی مدرن است. این نظریه به شکل موفقیت
آمیزی توضیح می دهد که چگونه افت و خیزهای کوانتومی خلاء، که در
حدود 36-10 ثانیه پس
از Big
bang بیگ بنگ شروع
می شود، می تواند به ساختار بزرگ-مقیاس جهان ما بیانجامد و منجر به
پیش گویی هایی شود که با گستره وسیعی از مشاهدات کیهانشناسی تایید
شده است. با این وجود کیهانشناسی تورمی نمی تواند نظریه ای نهایی
برای جهان باشد. بر طبق این نظریه اگر جهان را در زمان به عقب
برگردانیم، بسیار داغ و پر چگال می شود و در نتیجه قوانین فیزیک،
که تورم بر پایه آن بنا شده است (نسبیت عام کلاسیکی)، شکست می خورد.
در دوره زمانی مشهور به پلانک – که به یک ثانیه پلانک یعنی 43-10
ثانیه، بعد ازBig
bang بیگ بنگ می
رسد، نیروی گرانشی به مقادیر قابل مقایسه با نیروهای اساسی دیگر
رسیده و در این رژیم اثرات گرانش کوانتومی اهمیت می یابند و سبب
ایجاد شرایطی می شود که فراتر از فهم و درک سنتی از فضا و زمان است.
چه شرایطی مقدم بر تورم وجود داشته و تا چه حدی این شرایط پیش گویی
های مدل تورمی را تحت تاثیر قرار می دهد؟ چنین سوالات اساسی
کیهانشناسی بی پاسخ مانده اند، چون ما هنوز نظریه ای را سراغ
نداریم که با فیزیکِ پیش از نظریه تورم درگیر باشد و بتواند با
ملایمت آن را به دوره تورمی متصل کند. در مجله فیزیکال ریویو لترز
(PRL)، اگالوو و همکارانش در دانشگاه ایالتی پنسیلوانیا در پارک
دانشگاهی، گرانش کوانتومی حلقوی (LQG) - نظریه ای که نامزدی برای
گرانش کوانتومی محسوب می شود– را اتخاذ کرده و از آن برای بسط
سناریوی تورمی تا دوره پلانک مورد استفاده قرار داده اند.
نویسندگان این مقاله همچنین دریافتند که ویژگی های فاز پیش تورمیِ
در نظر گرفته شده، می تواند از یافته های کیهانشناختی قابل مشاهده
نیز نتیجه گردد. بنابراین از این طریق فرصتی برای آزمودن گرانش
کوانتومی و سنجش پیش تورمی در مشاهدات نجومی آینده فراهم می آید.
در دهه 1980 گاث، لینده،آلبرشت، و اشتاینهارت نظریه تورم
کیهانشناختی را برای توضیح دو معما در مدل Big
bang بیگ بنگ کیهانشناسی
پیشنهاد دادند: چرا جهان ما تقریباً تخت است (یعنی می تواند بعنوان
یک فضای اقلیدسی با انحنای بسیار بسیار کوچک توصیف گردد) و چرا
اینگونه به نظر می رسد که نواحی بسیار دور در جهان یک همبستگی
غیرتصادفی در دماهایشان دارند. مدل تورمی پاسخ هایی را برای این
سوالات فراهم می کند، با اصل قرار دادن اینکه جهان به سرعت با
فاکتور حداقل 1078،در دوره زمانی اولیه تحول کیهانی، بسط یافته است.
مدلهای بسیاری از تورم وجود دارد، اما به شکل کیفی همه آنها به
فیزیک مشابهی منجر می گردد: در طی تورم، افت و خیزهای کوانتومی
خلاء به افت و خیزهای چگالی منجر می شود که بعنوان بذرهای اولیه
ساختار بزرگ مقیاس جهان کنونی عمل کرده اند. چون این افت و خیزهای
چگالی همراه با افت و خیزهای دمایی هستند، نقش قابل مشاهده ای را
روی تابش زمینه ریز-موج کیهانی (CMB) می گذارند- به محض اینکه
انبساط جهان به فوتونها این امکان را بدهد که آزادانه در فضا حرکت
کنند، تابش حرارتی آزاد می شود. پیش گویی های بعمل آمده توسط نظریه
تورمی کاملاً با اندازه گیری های مدرن CMB تایید شده است.
برخلاف موفقیت های قابل ملاحظه ی نظریه تورمی، این نظریه مشکلات
مختلفی نیز دارد. اولین آنها "مسئله تکینگی" است. در سال 2003
بورده و همکارانش نشان دادند که مدل تورمی پیش بینی می کند که جهان،
در صورتی که از لحاظ زمانی به عقب باز گردد به یک نقطه چروکیده
میشود- تکینگی Big
bang بیگ بنگ- که در آن چگالی انرژی، انحنای فضا-زمان و دما
بینهایت هستند. چون نسبیت عام تحت این شرایط فرو می ریزد نظریه
تورمی با نزدیک شدن به نقطه تکینگی، نمی تواند معتبر باقی بماند.
مشکل دیگرِ مدل تورمی مسئله ی "ترانس-پلانکیان" است: بر اساس این
مدل مقیاس های کیهانشناختی جاری از ویژگی هایی نشأت می گیرند که
کوچکتر از طول پلانک در آغاز تورم است. طول پلانک ( فاصله طی شده
توسط نور در یک ثانیه پلانک) مقیاس طول طبیعی در دوره ی پلانک است.
اما در چنان مقیاس کوچکی، توصیف کلاسیکی فضا-زمان و گرانش نامعتبر
است.
در چگالی و انرژی های بالای رژیم پیش تورمی، انتظار می رود اثرات
نیروی گرانشی نیز نقش بازی کنند، تحت چنان شرایطی یک نظریه
کوانتومی جدید، برای توصیف ریز-ساختار فضا-زمان نیاز است؛ درست
شبیه راهی که مکانیک کوانتومی ریز-ساختار ماده را توصیف می کند.
گرانش کوانتومی حلقوی تلاشی است برای ترکیب مکانیک کوانتومی و
نسبیت عام. در این نظریه هندسه ی پیوسته کلاسیکی فضا-زمانی با
هندسه گسسته کوانتومی جایگزین می شود: می توان فضا را متشکل از "حلقه"
های محدود ریز در نظر گرفت.
در طول دهه گذشته، به امید درک فیزیک دوره پلانک و حل مشکلات
تکینگی مدلهای مختلفِ کیهانشناختی که شامل تورم می شوند، مدل LQG
بکار گرفته شده است (نظریه ای که بعنوان کیهانشناسی کوانتومی حلقوی
شناخته شده). اگرگسستگی فضا از چنان اهمیتی برخوردار نباشد،
معادلات LQG، مدلهای کلاسیکی کیهانشناسی را بی نهایت خوب تخمین می
زنند (شبیه پدیدار شدن مکانیک کلاسیک از مکانیک کوانتومی وقتی
اثرات کوانتومی قابل چشم پوشی باشند). با این وجود تفاوت ها زمانی
بارز می شوند که انحنای فضازمانی اهمیت یابد. درمدل LQG ، جهان از
تکینگی پدیدار نمی شود بلکه به جای "Big
bang بیگ بنگ" ، "جهش بزرگ" جایگزین می گردد یعنی: شروع دوره
انبساط به دنبال دوره ی انقباض فاز اولیه جهان.
در کاری که اگالوو و همکارانش انجام داده اند الگوی جهش LQG را
پذیرفته شده و مشکل تکینگی مرتفع می گردد. ایده اصلی این گروه
تحقیقاتی این است که در فاز نزدیک به جهش، افت و خیزهای خلاء در
طول یک هندسه فضا- زمانی غیر کلاسیکی و کوانتیده و در حجم کوچک
تقریباَ 103 مکعب طول پلانک رخ می دهد. این افت و خیزها به عنوان
بذرهای اولیه ساختار بزرگ-مقیاس جهان ما عمل می کنند. چون یک نظریه
کامل گرانش کوانتومی هنوز قابل دسترسی نیست این محققان بایستی
خودشان را به یک تقریب محدود می کردند: آنها افت و خیزها را با
استفاده از نظریه میدان کوانتومی استاندارد برطرف می کنند ( همانند
کیهانشناسی تورمی). آنان، مزیت نتایج اخیر را اخذ کرده و چگونگی
نمو و رشد این افت و خیزها در فضا زمانی که با تکینگی LQG کوانتیده
شده را مطالعه می کنند. چون الگوی تورمی از طریق LQG به دوره پلانک
توسعه می یابد، ناسازگاری ترانس-پلانکیان نیز حل می شود، چنانچه
LQG طولهای زیر-پلانک را به سختی مورد عمل قرار می دهد. بایستی
توجه کرد که سازگاری تحلیل آنها به یک فرض مهم متکی است: افت و
خیزهای خلاء کوانتومی، هندسه کوانتومی مورد نظر را تحت تاثیر قرار
نمی دهد. نویسندگان این مقاله نتیجه می گیرند که برای کلاس بزرگی
از شرایط اولیه ممکن، افت و خیزهای خلاء در آغاز تورم، شبیه آنچه
در تورم استاندارد مورد بررسی قرار گرفته است، یک مسئله اساسی
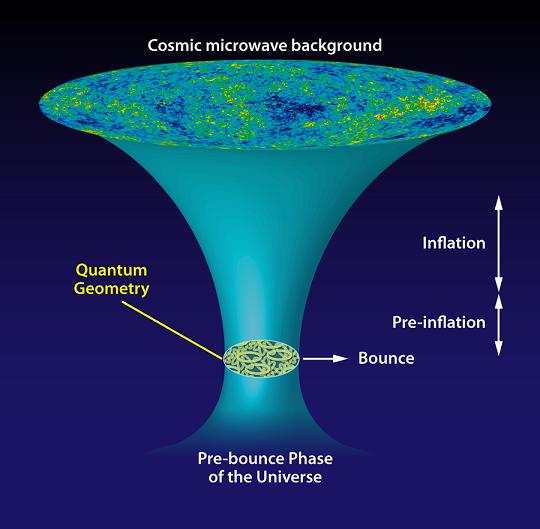
بشمار می رود. مدلِ بر پایه LQG ی آنها که به شکل شماتیک در شکل 1
نشان داده شده است، سازگار با پیشگویی های نظری تورمی است و آن را
به شکل پیوسته ای به دوره پلانک تعمیم می دهد.
با این وجود برای زیرمجموعه ای از چنان شرایط اولیه ای، حالت خلاء
ای که LQG پیش بینی کرده به شکل ماهرانه ای متفاوت از آن چیزی است
که در تورم فرض شده است. این موضوع به اثر قابل مشاهده بالقوه
گرانش کوانتومی می انجامد که می تواند در آزمایشات دقیق CMB ظاهر
شود؛ شبیه خواص آماری غیرگاوسی توزیع دمایی ( که اننظار می رود
مجزای از پیش گویی های مدل های تورمی استاندارد باشد). چنانچه
مشاهدات آینده پیش بینی های LQG را تایید کند دوره دور از دسترس
جهان اولیه برای کیهانشناسی، قابل دسترس خواهد بود.
با نگاه به جهان بسیار اولیه، زمانی که گرانش با دیگر نیروها هم
تراز بوده، می توان کلیدی را برای یک نظریه کاملاً سازگار بدست
آورد که نسبیت عام و مکانیک کوانتوم را متحد کند.
توضیح شکل طرح شماتیک تحول جهان بر اساس مدل اگالوو و همکارانش بر
پایه یک گرانش کوانتومی حلقوی LQG که بسط الگوی تورمی است. LQG
برای توصیف جهان اولیه دوره پلانک استفاده می شود. نویسندگان این
مقاله نشان می دهند که نظریه ی آنها با کیهانشناسی تورمی سنتی
ارتباط برقرار کرده و پیش گویی های مشابهی با ملاحظه زمینه میکرو
ویو کیهانی دارد. این مدل به جای "Big
bang بیگ بنگ" بر اساس "جهش بزرگ" بنا شده است: گزاری از یک
فاز انقباضی به یک فاز انبساطی جهان.
منبع: http://physics.aps.org/articles/v5/142
نقل از بیگ بنگ بلوگ اسکای
مرز بین ایمان و تجربه
نامه سرگشاده به
حضرت آیت الله هاشمی رفسنجانی
A Glance at the Earliest Universe
Parampreet Singh, Department
of Physics & Astronomy, Louisiana State University,
Baton Rouge, LA 70803, USA
Published December 17, 2012 | Physics 5,
142 (2012) | DOI: 10.1103/Physics.5.142
A new cosmological theory tackles the description of the
earliest era of the Universe, a period inaccessible by current
models.
Cosmological inflation, the hypothesis that the early Universe
underwent an extremely rapid expansion, is a popular paradigm in
modern cosmology. The theory successfully explains how quantum
mechanical fluctuations of the vacuum, starting about 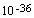 seconds
after the big bang, could have given rise to the large-scale
structure of our Universe, leading to predictions that have been
confirmed by a range of cosmological observations. However,
inflationary cosmology cannot be the ultimate theory of the
Universe. If one projects the Universe backward in time, it gets
so hot and dense that the laws of physics on which inflation is
based (classical general relativity) break down. In the
so-called Planck era, lasting up to one Planck second ( seconds
after the big bang, could have given rise to the large-scale
structure of our Universe, leading to predictions that have been
confirmed by a range of cosmological observations. However,
inflationary cosmology cannot be the ultimate theory of the
Universe. If one projects the Universe backward in time, it gets
so hot and dense that the laws of physics on which inflation is
based (classical general relativity) break down. In the
so-called Planck era, lasting up to one Planck second (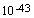 s)
after the big bang, the force of gravity would have reached
values comparable to the other fundamental forces. In this
regime, quantum gravity effects would have been important,
creating conditions that go beyond the conventional
understanding of space and time. s)
after the big bang, the force of gravity would have reached
values comparable to the other fundamental forces. In this
regime, quantum gravity effects would have been important,
creating conditions that go beyond the conventional
understanding of space and time.

Scheme of the evolution of the Universe according to the model
of Agullo et
al.,
based on a loop-quantum-gravity (LQG) extension of the
inflationary paradigm (figure is not to scale). LQG is used to
describe the early Universe of the Planck era. The authors show
that their theory smoothly connects with conventional
inflationary cosmology, delivering similar predictions regarding
the observable cosmic microwave background. The model is based
on a “big bounce” instead of a big bang: a transition from a
contracting to an expanding phase of the Universe.
What conditions existed prior to inflation and to what extent do
they affect the predictions of the inflationary model? Such
fundamental cosmological questions remain unanswered, since we
don’t yet have a theory that can tackle the physics of the
preinflation era and smoothly connect it to the inflationary
period. Writing in Physical
Review Letters, Ivan Agullo and colleagues at Pennsylvania
State University in University Park, take loop quantum gravity (LQG)—one
candidate theory of quantum gravity—and use it to extend the
inflationary scenario all the way to the Planck era [1].
The authors also find that features of the preinflationary phase
could result in observable cosmological signatures, thus
providing an opportunity to test quantum gravity and probe
preinflationary physics in future astronomical observations.
In the 1980s, Guth, Linde, Albrecht, and Steinhardt proposed the
theory of cosmological inflation [2]
to explain two puzzles in the big bang model of cosmology: why
our Universe is approximately flat (i.e., it can be described as
a Euclidian space, with a vanishingly small curvature) and why
very distant regions in our Universe appear to have a nonrandom
correlation in their temperatures (which suggests they were once
causally connected). Inflation provides answers to these
questions by postulating that the volume of the Universe rapidly
expanded by a factor of at least in
an early period of cosmic evolution. Many models of inflation
exist, but qualitatively they all lead to similar physics:
during inflation, quantum fluctuations of the vacuum lead to
density fluctuations that acted as the seeds of the large-scale
structure of the present Universe. Since these density
fluctuations were accompanied by temperature fluctuations, they
left an observable imprint on the cosmic-microwave-background (CMB)
radiation—the thermal radiation released once the Universe
expansion allowed photons to travel freely in space. The
predictions made by the inflationary theory have been largely
confirmed by state-of-the-art CMB measurements [3].
Despite its remarkable successes, the theory of inflation has
several problems. The first is the so-called “singularity
problem.” In 2003, Borde et
al. showed that
inflation predicts that the Universe, when evolved backward in
time, would shrink to a point—the big bang singularity—at which
energy density, spacetime curvature, and temperature are
infinite [4].
Since general relativity breaks down under these conditions, the
current inflationary theory cannot remain valid as the
singularity is approached. Another difficulty is the
“trans-Planckian” problem [5]:
according to inflation, current cosmological scales could have
developed from features that were smaller than the Planck length
at the onset of inflation. The Planck length (the distance
traveled by light in 1Planck
second) is the natural length scale in the Planck era. But on
such a small scale, the classical description of spacetime and
gravity is believed to be invalid.
At the high densities and energies of the preinflationary
regime, it is expected that quantum effects on the force of
gravity come into play. Under such conditions, a new quantum
theory of gravity, yet to be completed, is needed to describe
the “microstructure” of spacetime, similar to the way quantum
mechanics describes the microstructure of matter. Loop quantum
gravity is one such attempt to merge quantum mechanics and
general relativity. In LQG, the classical continuum geometry of
spacetime is replaced by a quantum discrete geometry: space can
be viewed as made of a fine fabric of finite “loops.”
Over the past decade, LQG has been applied to cosmology (a field
known as loop quantum cosmology), with the hope of understanding
Planck-era physics and solving the singularity problems of
different cosmological models, including inflation [6, 7].
When the discreteness of space does not matter, the equations of
LQG approximate classical models of cosmology extremely well
(much like quantum mechanics merges into classical physics when
quantum effects are negligible). Yet differences arise when the
curvature of the spacetime starts to be significant. In LQG, the
Universe does not emerge from a singularity. Instead, the big
bang is replaced by a “big bounce”: the beginning of a period of
expansion that followed a period of contraction of a previous
phase of the Universe [6].
The work of Agullo et
al. adopts the
bounce paradigm of LQG and thus it is free of the singularity
problem. Their key physical idea is that in the phase close to
the bounce, vacuum fluctuations occurred over a nonclassical,
quantized spacetime geometry in a tiny volume of approximately 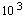 cubic
Planck lengths. These are the fluctuations that act as the seeds
of the large-scale structure of our Universe. Since a full
theory of quantum gravity is not yet available, the authors had
to restrict themselves to an approximation: they treat
fluctuations with standard quantum field theory (as in
inflationary cosmology), but they take advantage of recent
theoretical results [8]
and study how these fluctuations evolve in a spacetime that is
quantized by LQG techniques. Since the inflationary paradigm is
extended via LQG to the Planck-era, trans-Planckian
inconsistencies are also resolved, as LQG can treat rigorously
sub-Planck lengths. One should note that the consistency of
their analysis relies on one important assumption: the quantum
vacuum fluctuations do not, in turn, affect the underlying
quantum geometry. The authors show that this is true for a large
class of possible initial conditions, for which vacuum
fluctuations at the onset of inflation turn out to be
essentially the same as the ones considered in the standard
inflationary. Their LQG-based model, schematically illustrated
in Fig. 1, is thus consistent with the predictions of
inflationary theory and extends it in a continuous way to the
Planck era. cubic
Planck lengths. These are the fluctuations that act as the seeds
of the large-scale structure of our Universe. Since a full
theory of quantum gravity is not yet available, the authors had
to restrict themselves to an approximation: they treat
fluctuations with standard quantum field theory (as in
inflationary cosmology), but they take advantage of recent
theoretical results [8]
and study how these fluctuations evolve in a spacetime that is
quantized by LQG techniques. Since the inflationary paradigm is
extended via LQG to the Planck-era, trans-Planckian
inconsistencies are also resolved, as LQG can treat rigorously
sub-Planck lengths. One should note that the consistency of
their analysis relies on one important assumption: the quantum
vacuum fluctuations do not, in turn, affect the underlying
quantum geometry. The authors show that this is true for a large
class of possible initial conditions, for which vacuum
fluctuations at the onset of inflation turn out to be
essentially the same as the ones considered in the standard
inflationary. Their LQG-based model, schematically illustrated
in Fig. 1, is thus consistent with the predictions of
inflationary theory and extends it in a continuous way to the
Planck era.
However, for a narrow subset of such initial conditions, the LQG-predicted
vacuum state can be subtly different from the one assumed in
inflation. This would lead to potentially observable signatures
of quantum gravity [9]
that could be revealed in high-precision CMB experiments as
non-Gaussian statistical properties of the temperature
distribution (which are expected to be distinct from the
predictions of standard inflationary models). Should future
observations confirm LQG predictions, a so-far-inaccessible era
of the early Universe would become accessible to observational
cosmology.
Being able to look at the very early Universe, when gravity was
on par with the other forces, may well hold the key for a fully
consistent theory that unifies general relativity and quantum
mechanics.
References
-
I. Agullo, A. Ashtekar, and W. Nelson, “Quantum Gravity
Extension of the Inflationary Scenario,” Phys.
Rev. Lett. 109,
251301 (2012).
-
A. Guth, “Inflationary Universe: A Possible Solution to the
Horizon and Flatness Problems,” Phys.
Rev. D 23,
347 (1981); A. Linde, “A New Inflationary Universe
Scenario: A Possible Solution of the Horizon, Flatness,
Homogeneity, Isotropy, and Primordial Monopole Problems,” Phys.
Lett. B 108,
389 (1982); A. Albrecht and P. J. Steinhardt, “Cosmology
for Grand Unified Theories with Radiatively Induced 4
Symmetry Breaking,” Phys.
Rev. Lett. 48,
1220 (1982).
-
E. Komatsu et
al. (WMAP
Collaboration), “Seven-Year Wilkinson Microwave Anisotropy
Probe (WMAP) Observations: Cosmological Interpretation,” Astrophys.
J. Suppl. 192,
18 (2011).
-
A. Borde, A. H. Guth, and A. Vilenkin, “Inflationary
Space-Times Are Incomplete in Past Directions,” Phys.
Rev. Lett.90,
151301 (2003).
-
J. Martin and R. Brandenberger, “The Trans-Planckian Problem
of Inflationary Cosmology,” Phys.
Rev. D 63,
123501 (2001).
-
A. Ashtekar and P. Singh, “Loop Quantum Cosmology: A Status
Report,” Class.
Quant. Grav. 28,
213001 (2011).
-
M. Bojowald, “Loop Quantum Cosmology,” Living
Rev. Relativity 11,
4 (2008).
-
A. Ashtekar, W. Kaminski, and J. Lewandowski, “Quantum Field
Theory on a Cosmological, Quantum Spacetime,”Phys.
Rev. D 79,
064030 (2009).
-
I. Agullo and L. Parker, “Non-Gaussianities and the
Stimulated Creation of Quanta in the Inflationary Universe,” Phys.
Rev. D 83,
063526 (2011); I. Agullo and S. Shandera, “Large
Non-Gaussian Halo Bias from Single Field Inflation,” J.
Cosmol. Astropart. Phys. 1209,
007 (2012); J. Ganc and E. Komatsu, “Scale-Dependent
Bias of Galaxies and Mu-type Distortion of the Cosmic
Microwave Background Spectrum from Single-Field Inflation
with a Modified Initial State,” Phys.
Rev. D 86,
023518 (2012).
Source: APS
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
آخرین
مقالات |

