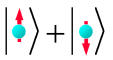نظریه سی پی اچ بر اساس تعمیم سرعت نور از انرژی به ماده بنا شده است.
سی پی اچ در ژورنالها
|
اعداد کوانتمی و اسپین
|
|||||
|
کره زمین دارای دو نوع حرکت وضعی و انتقالی است. حرکت آن به دور خورشید را حرکت انتقالی و چرخش زمین به دور خودش را حرکت وضعیمی گویند. هر یک از این دو نوع حرکت ، دارای اندازه حرکت زاویهای مخصوص به خود است.
حرکت انتقالی به دور خورشید، دارای اندازه حرکت زاویهای مداری و حرکت وضعی دارای اندازه حرکت زاویهای اسپینی (یا بطور اختصار اسپین) است. بدیهی است که اندازه حرکت زاویهای کل برابر با مجموع این دو اندازه حرکت است.
اگر مدلی را در نظر بگیریم که زمین فقط یک نقطه مادی باشد، نسبت دادن اسپین به آن بیمعنی خواهد بود. اما در مدل دیگری که زمین را با ابعاد محدود در نظر میگیریم، وجود اسپین نیز امکان پذیر است. لذا اگر این قضیه را در مورد مدل اتمی بوهر بکار ببریم، با این فرض که الکترون یک بار نقطهای نبوده، بلکه یک کره کوچک فرض شود، در این صورت الکترون علاوه بر اندازه حرکت زاویهای مداری (گردش به دور هسته) دارای اندازه حرکت زاویهای اسپینی (اسپین) نیز می باشد.
تائید تجربی اسپین الکترون حرکت چرخشی الکترون، نظیر حلقه جریانی است که گشتاور مغناطیسی خاص خود را دارد. اگر واقعا چنین گشتاور مغناطیسیی وجود داشته باشد، باید با میدان برهمکنش داشته و انرژی برهمکنشی متناظر این گشتاور مغناطیسی نیز وجود داشته باشد. این اثرها غیر از برهمکنش گشتاور مغناطیسی مداری با میدان مغناطیسی خارجی است. بعبارت دیگر در طول موج خطوط طیفی که از اتمها گسیل میشود، باید جابجایی در ترازهای انرژی آنها ظاهر شود که مربوط به اسپین الکترون باشد. در طیف سنجی های دقیق، چنین جابجائیهایی دیده شده است. این نوع آزمایشها و نیز شواهد تجربی دیگر نشان میدهند که الکترون ، تکانه زاویهای و گشتاور مغناطیسی دارد که به حرکت آن بر مدار پیرامون هسته مربوط نبوده، بلکه به ذات ذره مربوط است.
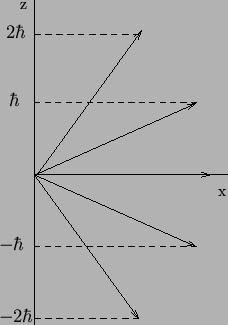
ویژگیهای اسپین تاسپین الکترون را با S نشان میدهند. مانند تکانه حرکت زاویهای مداری، این کمیت نیز کوانتیده است. بنابراین در میدان مغناطیسی، S هر جهتی را اختیار نمیکند و فقط مجاز است در جهت هایی قرار گیرد که مولفه آن در امتداد میدان مغناطیسی (اگر میدان مغناطیسی در جهت z فرض شود) ، مضرب 1/2 از ћ باشد. یعنی:
تفاوت بارز مولفه S_z (ناشی از اسپین) با مولفه z انداه حرکت زاویهای مداری ، در این است که اندازه حرکت زاویهای مداری برخلاف S_z مضرب صحیحی از ћ است.
مفهوم مقدار اسپین برای درک اینکه مکانیک کوانتومی چه چیزی در باره ی اسپین ذره مطرح می کند، باید سرعت دوران اصلی و رابطه ی اسپین را با آن توضیح داد.این یک واحد بنیادی است که اسپین واقعی ذره بر حسب آن اندازه گیری می شود. مکانیک کوانتومی می گوید که چگونه این سرعت را برای هر ذره محاسبه کنیم. برای مطالعه بیشتر در این زمینه جرم اصلی و اسپین را مطالعه کنید.
اسپین الکترون در مکانیک کوانتومی در مکانیک کوانتومی که تابع موج جانشین مدارهای بوهر میشود، ارائه تصویری از چرخش الکترون غیر ممکن است. اگر توابع موج الکترون را مانند تودههای ابری تصور کنیم که پیرامون هسته قرار گرفتهاند، میتوان تعداد بیشماری پیکان بسیار کوچک را در نظر مجسم کرد که در درون توده ابری پراکندهاند و همگی در یک راستا ، z+ یا z- امتداد دارند. البته آنچه گفته شد یک تصور خیالی است و امیدی به دیدن ساختار اتمی وجود ندارد. چون ابعاد آن هزاران مرتبه از طول موجهای نور کوچکتر است. همچنین برهمکنش فوتونها با اتم ، ساختاری را که دیدن آن مورد نظر است، بشدت تغییر میدهد. در هر حال ، مفهوم اسپین الکترون با آزمایشهای متعدد تجربی مورد تائید قرار گرفته است و در مکانیک کوانتومی برای مشخص کردن عدد کوانتومی جدیدی به نام عدد کوانتومی اسپینی الکترون در نظر گرفته میشد.
ساختار ریز شکافت تراز انرژی در اثر گشتاور مغناطیسی اسپین الکترون در نبود میدان خارجی را جفت شدگی اسپین مدار مینامند. چون اسپین الکترون با میدان مغناطیسی ناشی از اندازه حرکت زاویهای مداری (حرکت الکترون پیرامون هسته) برهمکنش میکند. در مکانیک کوانتومی با استفاده از حل معادله شرودینگر مقدار این شکافتگی را میتوان تعیین نمود. شکافتگیهایی را که از این نوع برهمکنش مغناطیسی در خطوط طیف مربوط به اتمهای مختلف ایجاد میشوند، در مجموع ساختار ریز میگویند.
البته شکافتگیهای به مراتب کوچکتر دیگری نیز وجود دارند که حاصل برهمکنش گشتاور مغناطیسی هسته با تکانه زاویهای مداری و اسپین الکترون هستند و ساختار فوق ریز نام دارد.
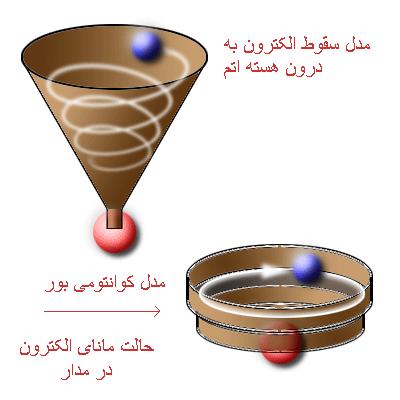
اعداد کوانتومی در بررسی ساختار اتم مدلهای مختلفی ارائه شده است. ابتداییترین این مدلها ، مدل سیارهای رادرفورد است. بعد از مدل سیارهای رادرفورد ، نیلز بوهر مدل جدیدی را ارائه داد (مدل اتمی بوهر). این مدل میتوانست ساختار طیفی اتم هیدروژن را توضیح دهد. در اصل موضوع بوهر که اساس و مبنای مدل بوهر است، فرض بر این است که الکترونها مقیدند در مدارهایی حرکت کنند که در آنها اندازه حرکت الکترون مضرب درستی از ћ است.همچنین در این مدل فرض میشود که ترازهای انرژی کوانتیدهاند. بعدها که ساختار طیف مربوط به عناصر مختلف مورد توجه قرار گرفت، انرژی هر الکترون در اتم را با یک سری اعداد که اعداد کوانتومی نامیده می شوند، مشخص کردند.
بنابر نظریه الکترومغناطیس هرگاه ذره ی بارداری شتاب بگیرد، انرژی الکترومغناطیسی تابش می کند. بنابراین الکترونی که در ساختمان اتم دارای شتاب است می بایست در هسته سقوط می کرد. در مدل اتمی بور که ترازهای مجاز انرژی را مطرح کرد، این مشکل برطرف شد.
عدد کوانتومی اصلی گفتیم که ترازهای انرژی در اتم گسسته (کوانتومی) هستند. یعنی اگر اتم توسط تابش الکترومغناطیسی بمباران شود، تابش توسط الکترونها جذب میشود و الکترونها از ترازهای اولیه یا پایه خود تحریک شده و به ترازهای برانگیخته میروند. اما چون این حالت یک حالت ناپایدار است، لذاالکترون با گسیل تابش از تراز برانگیخته به تراز اولیه خود برمیگردد. مقدار انرژی جذب شده یا گسیل شده متناسب با فاصله ترازهای انرژی است.یعنی اگر انرژی تراز اولیه را با E و انرژی تراز برانگیخته را با 'E مشخص کنیم، در این صورت فرکانس نور گسیل شده یا تحریک شده از رابطه E - E΄ = hv حاصل میشود.
اگر با تقریب مدار حرکت الکترون به دور هسته را دایرهای به شعاع r فرض کنیم، با توجه به این که نیروی وارد شده از طرف هسته بر الکتروننیروی جانب مرکز است، لذا اگر بار هسته را برابر Ze در نظر بگیریم که در آن z عدد اتمی است، مقدار نیروی وارد بر الکترون با توجه به قانون کلمب برابر:
F=-kZe2/r2
خواهد بود که در آن r شعاع مدار دایراه ای است. اما طبق قانون دوم نیوتن نیروی جانب مرکز برابر است با:
F=-mv2/r
با مساوی قرار دادن طرف راست دو معادله اخیر خواهیم داشت:
mv2/r=kZe2/r2
(1) mv2=kZe2/r
که در این رابطه v سرعت الکترون و m جرم آن است. از طرف دیگر انرژی پتانسیل الکترون برابر است با:
Ep=-kZe2/r
مجموع انرژی جنبشی الکترون 1/2mv2 و انرژی پتانسیل آن برابر انرژی کل الکترون است. پس برای انرژ کل خواهیم داشت:
E= 1/2mv2-kZe2/r
و با در نظر گرفتن رابطه ی (1) خواهیم داشت:
E=-kZe2/2r
علامت منفی به دلیل مقید بودن الکترون در نظر گرفته شده است. از طرف دیگر ، چون طبق اصل موضوع بوهر ، اندازه حرکت الکترون باید مضرب صحیحی از ћ باشد، در این صورت:
mvr=nћ
خواهد بود. n یک عدد طبیعی است و عدد کوانتومی اصلی نامیده میشود. که تنها می تواند مقادیر ...,n=1,2,3 را داشته باشد.
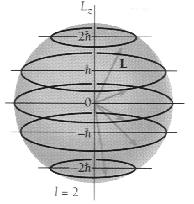
عدد کوانتومی اندازه حرکت زاویهای مداری عدد کوانتومی n که یک عدد صحیح و مثبت است، بزرگی اندازه حرکت زاویهای الکترون به دور هسته را بر اساس اصل موضوع بوهر ، طبق رابطه L=nћ مشخص میکند. اما از دیدگاه مکانیک موجی درست نیست که برای الکترون یک مسیر مشخص دایرهای یا شکل دیگری را در نظر بگیریم. (اصل عدم قطعیت مانع این کار است) و نیز از این دیدگاه قاعده بوهر در مورد کوانتش بزرگی اندازه حرکت زاویهای درست نیست. بر خلاف نظریه کلاسیک ، مکانیک موجی نشان میدهد که بزرگی اندازه حرکت زاویهای مداری (L) یک دستگاه اتمی کوانتیده است و مقادیر ممکن آن میتواند از رابطه:
بدست آید. در این رابطه l عدد صحیحی است که عدد کوانتومی اندازه حرکت زاویهای مداری نامیده میشود. برای مقدار مفروض از عدد کوانتومی اصلی n خواهیم داشت:
الکترون با جذب انرژی از مدار پائین به مدار بالا جهش می کند.
در نمادگذاری ترازها هر مقدار از l با یک حرف مشخص میشود. در این نمادگذاری مقدار l=0 با حرف s و l=1 با حرف p و l=2 با حرف d و ... مشخص می شود. چون انرژی فقط برحسب عدد کوانتومی اصلی مشخص میشود، بنابراین در مورد تک الکترونی که تحت تأثیر یک نیروی کولنی از جانب هسته است و در تراز n=3 , l=0,1,2 دارای انرژی یکسانی خواهند بود.
اعداد کوانتومی مغناطیسی مداری گفتیم که الکترون در اثر نیرویی که از طرف هسته بر آن وارد میشود، حول هسته میچرخد. چون الکترون یک ذره باردار است، بنابراین مدار الکترون را میتوان یک مدار مغناطیسی در نظر گرفت. برای این مدار مغناطیسی و در واقع برای الکترون میتوان یک گشتاور دو قطبی مغناطیسیتعریف نمود. این کمیت بر اساس اندازه حرکت زاویهای مداری الکترون تعریف میشود که از رابطه ی زیر به دست می آید.
حال اگر یک میدان
مغناطیسی خارجی بر
آن اعمال
شود، در این صورت میدان سعی میکند تا گشتاور دو قطبی
مغناطیسی و به تبع آن L را
در راستای میدان قرار دهد، اما در مکانیک موجی بردار
اندازه حرکت زاویهای مداری L نمیتواند
هر جهتی را نسبت به میدان مغناطیسی اختیار کند، بلکه
محدود به جهتهای به خصوصی است که برای آن مؤلفه بردار
اندازه حرکت زاویه مداری، در
راستای میدان مغناطیسی ، مضرب دستی از ћ باشد.
بنابراین اگر جهت میدان مغناطیسی را در راستای محور z اختیار
کنیم، در این صورت مؤلفه z بردار L از
رابطه Lz =
ml ћ حاصل
میشود. در این رابطه ml عدد
کوانتومی مغناطیسی مداری است.
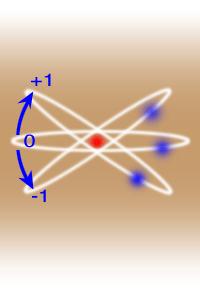
به ازای یک مقدار مفروض l ، ml میتواند
مقادیر زیر را اختیار کند: { ml ={-l , -l + 1 , -l + 2 , … , 0 , …l-1 , l
عدد کوانتومی مغناطیسی اسپینی
در نظریه کوانتومی سه ثابت فیزیک
کلاسیک مربوط به حرکت ذرهای که تحت تأثیر جاذبه عکس
مجذوری قرار دارد، کوانتیدهاند. این سه ثابت عبارتند
از: انرژی ، بزرگی
اندازه حرکت زاویهای مداری و مؤلفه
اندازه حرکت زاویهای مداری در یک جهت ثابت از فضا. در
مکانیک کوانتومی به این ثابتهای حرکت اعداد کوانتومی n
و l و
ml نسبت
داده میشوند، اما علاوه بر این سه عدد کوانتومی ،
عدد کوانتومی دیگری به نام عدد کوانتومی
اسپینی که
به مفهوم اسپین
الکترون مربوط
است، معرفی میشود. اصل طرد پاولی وقتی که مدل اتمی بوهر با موفقیت ارائه و پذیرفته شد، این پرسش مطرح شد که الکترونها در سیستم سنگین چگونه سازمان پیدا میکنند؟ معادله شرودینگر هیچگونه جواب قانع کنندهای برای این پرسش نداشت. چون مطابق این معادله اگر دمای یک سیستم را به دمای نزدیک به دمای صفر مطلق نزدیک کنیم آنگاه انتظار میرود که تمام الکترونهای یک اتم به پایینترین سطح انرژی یعنی n=1 منتقل میشوند. اما نتایج تجربی طیف شناس ها را نمی توان با این فرض توضیح داد. تا اینکه فردی به نام ولفگانگ پائولی توانست این معما را حل کند. وی نظریهای پیشنهاد داد که امروزه با عنوان اصل ترد پائولی شناخته می شود. مطابق این اصل در یک اتم در حالت پایه، هیچ دو الکترونی را نمی توان یافت که هر چهار عدد کوانتمی آن ها یعنی:
n, l , m, s
یکسان باشد. بین هر جفت الکترون حداقل یکی از این اعداد متفاوت از دیگری است، این بیان اصل طرد پائولی در مدل اتمی بوهر است.
منابع
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
|
Sub quantum space and interactions from photon to fermions and bosons |
|
نامه سرگشاده به حضرت آیت الله هاشمی رفسنجانی |
آرشیو موضوعی

از آغاز کودکی به پدیده های فیزیکی و قوانین حاکم بر جهان هستی کنجکاو بودم. از همان زمان دو کمیت زمان و انرژی بیش از همه برایم مبهم بود. می خواستم بدانم ماهیت زمان چیست و ماهیت انرژی چیست؟