مقدمه:
یکی از
مهمترین دستاوردهای نسبیت عام انحنای فضا -زمان
بود. اینشتین در سال 1915 با ارائه نسبیت عام، نسبیت
خاص را از دستگاه های لخت به دستگاه های شتابدار تعمیم
داد. نتیجه ی مستقیم این تعمیم پیشگویی انحنای فضا
بود. در این نوشته نخست سعی می شود انحنای فضا توضیح
داده شود و سپس خواهیم دید که نظریه سی. پی. اچ. چگونه
انحنای فضا را توجیح می کند. اما قبل از آن یادآوردی
برخی مفاهیم ضروری است.
نسبیت
عام
نسبيت عام بر اساس اصل هم ارزي تدوين
شد.
اصل هم ارزي:
قوانين
فيزيک در يک ميدان جاذبه يكنواخت و در يک دستگاه كه با
شتاب ثابت حركت مي کند، يكسان هستند.
به عنوان مثال فرض کنيم يک دستگاه
مقايسه اي با شتاب ثابت در حركت است. مشاهدات در اين
دستگاه نظير مشاهدات در يک ميدان گرانشي يكنواخت است
در صورتي كه شدت ميدان گرانشي برابر شتاب دستگاه باشد،
يعني a=-g باشد،
در اين صورت مشاهدات يكسان خواهد بود.
فرض کنیم یک سفینه با شتاب بطرف بالا
(نسبت به زمین) در حرکت است. بطوریکه:
a=-g
در اینصورت تمام مشاهدات سرنشین سفینه
نظیر مشاهدات ناظر روی زمین است. اگر سرنشین سفینه
جسمی را رها کند، چنین مشاهده می کند که آن جسم با
شتاب بطرف سطح سفینه حرکت می کند. یک پرتو نوری که از
یکطرف سفینه وارد شود، در مدتیکه این پرتو بسمت دیگر
سفینه می رسد، سفینه مسافتی را طی می کند که این مسافت
موجب می شود، پرتو نور، به نقطه ی مقابل نرسد و کمی
پایین تر از آن به سطح مقابل برخورد کند. شکل زیر
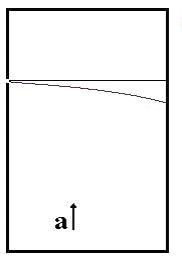
بنابراین مسیر نور در سفینه خط مستقیم
نیست، بلکه منحنی است. لذا مسیر نور در یک میدان
گرانشی نیز بایستی خمیده باشد.
در سال 1919 انحناي فضا را هنگام کسوف
کامل خورشيد با نوري که از طرف ستاره ي مورد نظري به
سوي زمين در حرکت بود و از کنار خورشيد مي گذشت مورد
تحقيق قرار دادند که با پيشگويي نسبيت تطبيق مي کرد.
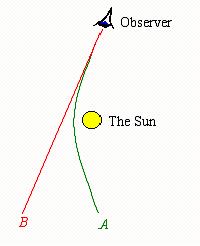
مسیر نور هنگام عبور از میدان گرانشی
خمیده می شود.
اين موفقيت بسيار بزرگي براي نسبيت
بود. از آن زمان به بعد توجه به ساختار هندسي و خواص
توپولوژيک فضا، بررسي واقعيت هاي فيزيکي را به حاشيه
راند. مضافاً اينکه گرانش را از فهرست نيروهاي اساسي
طبيعت در فيزيک نظري حذف کرد.
بنا بر نسبيت، گرانش اثر هندسي جرم بر
فضاي اطراف خود است. كه فضا- زمان ناميده مي شود. يعني
جرم فضاي اطراف خود را خميده مي كند.
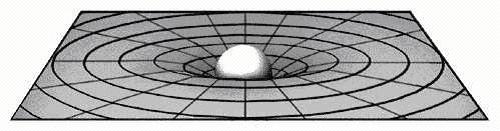
اینشیتن تلاش کرد ساختار هندسی فضا را
بصورت معادلات ریاضی بیان کند. بهمین دلیل از هندسه ی
نااقلیدسی ریمان (هندسه ی بیضوی) بهره گرفت و معادلات
میدان را ارائه کرد. در
اینجا سه نکته بسیار مهم قابل توجه است:
1 - معادلات
میدان نظریه نسبیت به صراحت از اصل هم ارزی نتیجه نمی
شود، بلکه ساده ترین معادلاتی است که با نسبیت توافق
دارد.
2 - توضیح
فیزیکی برای انحراف مسیر نور در میدان گرانشی ارائه
نشده است. هرچند بحث دستگاه ها نیز یک روش فیزیکی برای
توضیح پدیده ها است، اما اینکه میدان گرانشی چه تاثیر
بر روی فوتون می گذارد که مسیر پرتو نوری خمیده می
شود، مسئله ی دیگری است که نسبیت در مورد آن سکوت کرده
است.
3- فضا-زمان
در نسبیت کمیتی پیوسته است. در حالیکه تغییر انرژی و
اصولاً تولید انرژی کوانتومی است. لذا با فضا-زمان
پیوسته نمی توان تغییرات گسسته ی انرژی فوتون را توجیح
کرد.
بنابراین در
ادامه تلاش می شود توجیه فیزیکی انحنای فضا با توجه به
ساختمان فوتون بررسی گردد.
سطوح هم
پتانسیل
یک میدان را
در نظر بگیرید. بسته به اینکه شما چه میدانی را در نظر
گرفته اید و کدام ویژگی را برای این میدان تعریف کرده
اید، تمام نفاطی از فضا را که دارای این ویژگی و برابر
هستند، سطح هم پتانسیل می گوییم. به عنوان مثال؛ فرض
کنیم در یک اطاق بخاری روشن و در حال انتشار گرما است.
هرچه به بخاری نزدیکتر شویم، دما بیشتر خواهد شد. تمام
نقاط اطاق که دارای درجه حرارت یکسانی (مثلاً 20 درجه)
هستند، تشکیل یک سطح هم پتانسیل در این میدان حرارتی
می دهند.
حال میدان
گرانشی را در نظر بگیرید. شدت گرانش از نقطه ای به
نقطه دیگر در این میدان احتمالاً تغییر می کند. اما
نقاطی در این میدان وجود دارند که از نظر شدت میدان
گرانشی برابرند، مجموعه همه ی این نقاط را سطح هم
پتانسیل می گوییم. شکل زیر
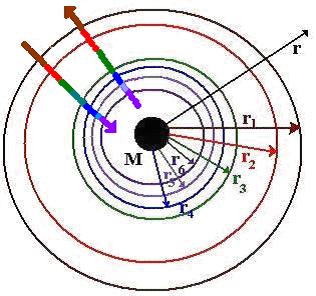
در شکل بالا
فرض شده که جسم کاملاً کروی است. این جسم در فضای
اطراف خود میدان گرانشی ایجاد کرده و با توجه به رابطه
ی g=GM/r2 تمام
نقاطی از فضا که بر روی یک کره بمرکز مشترک جسم و آن
کره قرار دارند، دارای پتانسیل گرانشی برابر هستند و
تشکیل یک سطح هم پتانسیل می دهند. در این شکل کره بنفش
(که در شکل بصورت دایره نشان داده شده است) یک سطح هم
پتانسیل است که شدت گرانش در تمام نقاط واقع بر این
سطح فرضی، برابرند.
بهمین ترتیب
کره های سبز، قزمز... همه تشکیل یک سطح هم پتانسیل
گرانشی می دهند. بدیهی است که پتانسیل این کرات با هم
برابر نیستند، اما هرکدام یک سطح هم پتانسیل گرانشی را
شکل می دهند.
حال به سقوط
و صعود فوتون در میدان گرانشی توجه کنید. همچنانکه که
در فصول گذشته بطور مفصل بحث شد، هرگاه فوتون در یک
میدان گرانشی سقوط کند، انرژی آن افزایش می یابد که
جابجایی بسمت آبی گرانش نامیده می شود. و هنگام صعود
انرژی آن کاهش می یابد که جابجایی بسمت سرخ است. در
شکل بالا عبور فوتون از سطوح مختلف پتانسیل گرانشی
موجب تغییر فرکانس (انرژی) آن می شود. با کاهش فصله از
جسم، جابجایی بسمت آبی و با افزایش فاصله جابجایی بسمت
سرخ است.
حال باید
ببینیم این پدیده را همراه با انحنای فضا چگونه می
توان با نظریه سی. پی. اچ. توجیه کرد.
انحنای
فضا از دیدگاه نظریه سی. پی. اچ.
فرض کنیم یک
فوتون از فضای بسیار دور نسبت به یک جسم، وارد میدان
گرانشی آن می شود. همانطور که می دانیم فوتون با سرعت
نور و روی خط مستقیم حرکت می کند و فاصله را بصورت
حاصلضرب سرعت در زمان نسبت به دستگاه لخت طی می کند.
شکل زیر

مسیر نور در
فضا و دور از میدان گرانشی از دید ناظر لخت
هرچند که
نمی توان فضای تهی آرمانی، یعنی جایی که میدان گرانشی
وجود نداشته باشد یافت، اما فرض می کنیم گرانش جنان
ضعیف است که اثر قابل توجهی بر روی نور ندارد.
حال این
پرتو نوری وارد میدان گرانشی می شود. تحت تاثیر میدان
گرانشی قرار می گیرد و مانند یک ذره ی جرم دار در
میدان گرانشی رفتار می کند. زیرا فوتون دارای انرژی و
جرم و اندازه حرکت است که از رابطه ی زیر به دست می
آید.

در غیاب
میدان گرانشی، همه مقادیر بالا وابسته به فوتون ثابت
می ماند. اما در میدان گرانشی تغییر می کند و این
تغییرات تابع شدت میدان گرانشی یا عبور از یک سطح هم
پتانسیل به سطح هم پتانسیل دیگر است.
طبق نظریه
سی. پی. اچ.، میدان گرانشی از بار-رنگها تشکیل می شود
که با ورد بار-رنگ به ساختمان فوتون انرژی آن افزایش
می یابد و با خروج بار-رنگ، انرژی فوتون کاهش می یابد.
از طرف دیگر بار-رنگها نیز دارای تکانه و انرژی جنبشی
هستند و هنگام ورود بار-رنگ به ساختمان فوتون، تکانه ی
آن نیز موثر است و تکانه ی فوتون را تغییر می دهد که
با توجه به طول موج دوبروی بسادگی قابل توضیح است.
زیرا با ورود بار-رنگ به ساختمان فوتون و افزایش انرژی
فوتون، فرکانس آن نیز افزایش می یابد و در نتیجه طول
موج کاهش یافته و بنابراین تکانه نیز طبق رابطه بالا
افزایش می یابد.
از طرف دیگر
تغییر تکانه با نیروی وارد شده متناسب است. لذا با
توجه به جهت حرکت بار-رنگها، جهت نیروی وارد بر فوتون
نیز مشخص می شود. شکل زیر
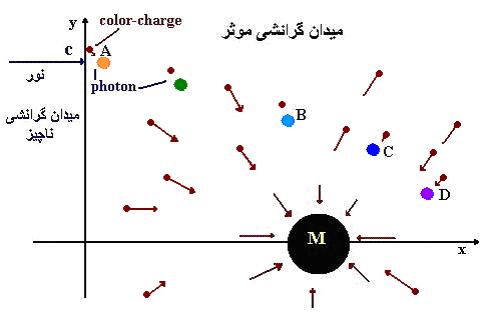
هنگامیکه
فوتون وارد میدان گرانشی می شود، تحت تاثیر بار-رنگها
قرار می گیرد. جهت حرکت تمام بار-رنگها بطرف جسم عامل
میدان گرانشی است. بنابراین با توجه به موقعیت مکانی
فوتون و جهت حرکت بار-رنگ Aورودی
می توان مسیر جدید فوتون را مشخص کرد. در نقطه
فوتون با
اولین بار-رنگ کنش خواهد داشت. جهت حرکت فوتون با محور
افقی هم جهت است و جهت حرکت بار- M رنگ
بطرف مرکز جسم
است. در
همین نقطه جهت حرکت فوتون تغییر می کند و در راستای
محور عمودی منحرف می شود. در نقاط بعدی نیز بهمین
ترتیب مسیر حرکت فوتون دائماً تغییر می کند و بصورت
منحنی در می آید.
کنش
بار-رنگ و فوتون
حال فوتونی
را در نظر بگیریم که با یک بار-رنگ کنش دارد و بار-رنگ
وارد ساختمان فوتون می شود. به جهت حرکت بار-رنگ و
فوتون دقت کنید. شکل زیر
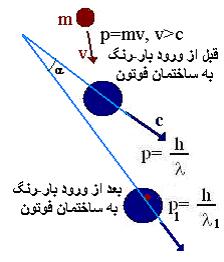
با ورود
بار-رنگ به ساختمان فوتون، یک فوتون جدید خواهیم داشت
با انرژی جدید، جهت حرکت جدید و اندازه حرکت جدید.
بایستی توجه داشت که در این فرایند تمام قوانین بقا
محفوظ می مانند. با این نگرش بخوبی واضح است که چرا
مسیر نور در میدان گرانشی خمیده است. حال با توجه به
خمیدگی مسیر نور می توانیم این مسیر را بصورت یک حرکت
دو بعدی و منحنی شکل در نظر بگیریم و آن را با توجه به
شرایط محیطی مورد بررسی قرار دهیم.
انحنای
منحنی دو بعدی
فرض کنیم
متحرکی در صفحه دارای حرکت منحنی شکل است. مسیر حرکت
این متحرک را می توان بصورت کلی زیر نشان داد.
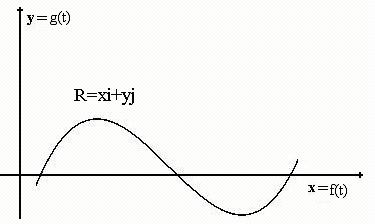
|
توابعی
پارامتری از متغییر دیگری هستند
|
x, y |
در اینصورت
انحنای منحنی در هر نقطه ی دلخواه واقع بر آن از رابطه
ی زیر به دست می آید:
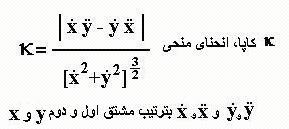
مسیر نور در
میدان گرانشی را می توان یک منحنی در فضای دو بعدی در
نظر گرفت و با توجه به شدت میدان گرانشی انحنای آن را
بر حسب زمان به دست آورد. اما این کار چندان ساده ای
نیست.
مشکلات
تعیین انحنای فضا
برای تعیین
انحنای منحنی مسیر نور (یا انحنای فضا) در میدان
گرانشی سه مشکل اساسی وجود دارد:
1 - زمان
کمیتی مطلق نیست. بنابراین معادله مسیر که خود تابع
زمان است، باید با توجه به تاثیر گرانش بر زمان مورد
توجه قرار گیرد. در نظریه سی. پی. اچ.، زمان تابع
نیروهای خارجی است و اصولاً زمان به دلیل وجود نیروهای
خارجی پدید می آید. اما فعلاً برای اجتناب از اطاله ی
کلام وارد چگونگی آن نمی شویم و به نگرش نسبیت به زمان
در میدان گرانشی توجه می کنیم.
در نسبیت،
زمان تابع پتانسیل گرانشی است و هرچه شدت گرانشی بیشتر
باشد، ساعت کندتر کار می کند. فرض کنیم یک ساعت در سطح
زمین قرار داشته باشد و ساعت دیگری در بالای جو (مثلاً
در یک ایستگاه فضایی)، چون شدت گرانشی در سطح زمین
بیشتر از بالای جو است، ساعت ساکن روی زمین کندتر از
ساعت بالای جو کار خواهد کرد. اصولاً می توان اختلاف
آهنگ ساعت ها را از روی اختلاف پتانسیل تعریف کرد. به
رابطه ی زیر توجه کنید:
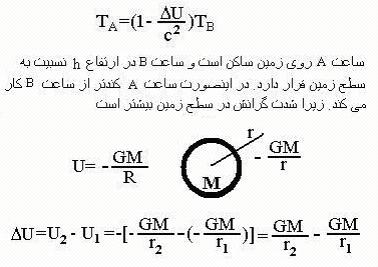
بنابراین با
سقوط فوتون و کاهش ارتفاع آن نسبت به سطح جسم، آهنگ
زمان در محل حرکت فوتون کاهش می یابد و نمی توان در
رابطه ی ct زمان
را مانند دستگاه لخت در نظر گرفت.
2 - با
تغییر سطح پتانسیل (شدت میدان گرانشی)، با در نظر
گرفتن رابطه ی زمان (شکل بالا) ضریب تبدیل زمانها از
دید ناظر ساکن بر سطح جسم (یا هر ناظر دیگری) نیز
تغییر می کند، زیرا فاصله تغییر می کند که در آهنگ
ساعت موثر است.
3 - جهت
حرکت فوتون (پرتو نوری) دائماً در حال تغییر است.
تغییر جهت حرکت و تغییر شدت میدان گرانشی تواماً موجب
می شود حرکت فوتون روی هر دو محور افقی و قائم، حرکتی
با شتاب متغییر باشد. لذا خواهیم داشت:
x=f(t, r, q)
, y=g(t, r, q)
لذا معادله
ی حرکت روی هر دو محور شتابدار، با شتاب متغییر است.
شتاب گرانش را در هر نقطه از مسیر می توان بصورت:
g=GM/r2
در نظر
گرفت. تنها باید مولفه های افقی و عمودی آن را جدا
کرد. اما زاویه نیروی وارد بر فوتون هرچند در محاسات
نقش مهمی دارد، اما یک کمیت اساسی مربوط به فضای مورد
مطالعه نیست. ولی زمان و گرانش، چزء غیر قابل تفکیک از
ویژگیهای فضا هستند. لذا ما بطور کلی در فضای پنچ بعدی
بسر می بریم. بهیچ وجه نمی توانیم هیچ یک از دو کمیت
زمان و نیرو را نادیده بگیریم. لذا در حالت کلی باید
پنج بعد را در معادلات منظور داشت، سه بعد برای فضای
تهی، یک بعد برای نیرو و یک بعد نیز برای زمان. و هر
تابعی که بخواهد مسیر حرکت را بطور واقعی مورد بررسی
قرار دهد، الزاماً باید بشکل توابع پنج بعدی فرمول
بندی شود، یعنی: (x,
y, z, f, t) ما
در این مورد خاص حرکت را تنها در دو بعد در نظر می
گیریم و باید معادلات را بصورت:(x,
y, f, t) فرمولبندی
کنیم. همچنین در مورد مسیر که کمیتی پیوسته است،
تاثیری در ویژگی گسستگی فضا-نیرو-زمان نخواهد داشت.
واقعیت این است که فضای مادی خود گسسته است. زیرا ما
با رفتار ذرات و ویژگی آنها و کنش مقابل بین آنها
سروکار داریم. اصولاً فضای بدون ماده چیز قابل تصوری
نیست و هر برداشتی از فضا به نوعی با مفاهیم مادی در
هم می آمیزد. ماده به هر شکلی که ظاهر شود، خود از
کوانتومها یا زیر کوانتومها و یا ترکیبی از آنها تشکیل
می شود. بنابراین بررسی فضای فیزیکی با نگرش ریاضی به
مختضات فضایی تفاوت کلی دارد. و فضای فیزیکی کوانتیده
است.
معادلات
حرکت نور در میدان گرانشی
فوتونی را
در نظر بگیرید که در میدان گرانشی با بار-رنگها
(گراویتونها یا گرانش) در کنش متقابل است. (شکل زیر)
بار-رنگها با اندازه ی حرکتی که دارند وارد ساختمان
فوتون می شوند و اندازه حرکت فوتون تغییر می کند.
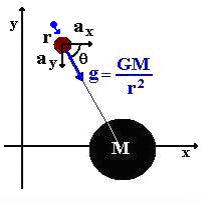
در حالت کلی
تغییر سرعت مترادف است با اعمال نیرو و تغییر اندازه ی
حرکت. ورود بار-رنگ به ساختمان فوتون طول موج و در
نتیجه اندازه ی حرکت آنرا تغییر می دهد. تغییر اندازه
ی حرکت در حالت کلی روی هر دو محور انجام می گیرد.
تغییر اندازه ی حرکت فوتون می تواند هم از نظر مقدار
سرعت باشد و هم از نظر جهت سرعت. اما در اینجا تغییر
مقدار سرعت مد نظر نیست و تنها از نظر تغییر جهت سرعت
مورد مورد بررسی قرار می گیرد.
در مدت
زمان کوتاهی که بار-رنگ وارد ساختمان فوتون می شود،
مجموعه ی فوتون و بار-رنگ دارای شتاب هستند. این شتاب،
تابع شدت میدان گرانشی است، زیرا چگالی بار-رنگ ها
تعیین کننده ی شدت میدان گرانشی در هر نقطه از فضا
است.
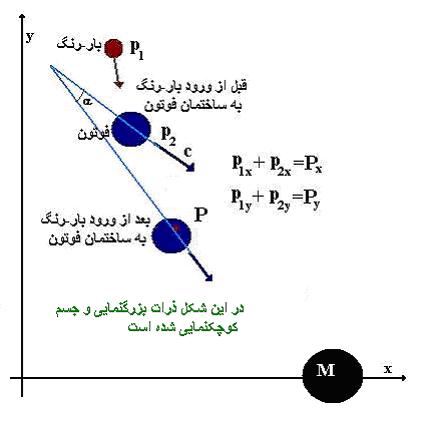
با توجه به
نمودار بالا و تغییر اندازه حرکت و انرژی فوتون می
توان معادلات مربوطه را به دست آورد.
فرض کنیم
فوتون با جرم و اندازه حرکت P1 ,
m1 در
مسیر خود با تعداد n بار-رنگ
کنش دارد. جرم و اندازه حرکت هر بار-رنگ برابر است با pi ,
m
بار-رنگها
همگی دارای جرم برابر ولی اندازه ی حرکت متفاوت هستند.
زیرا اندازه ی حرکت کمیتی برداری است. کنش بین فوتون و
بار-رنگها را در صفحه و روی دو محور در نظر می گیریم.
شکل زیر

همجنانکه در
روابط بالا نشان داده شده اندازه ی حرکت فوتون روی هر
دو محور تغییر می کند. چون انتخابxمحورها
اختیاری است، محور افقی را
طوری انتخاب می کنیم ناظر و چشمه نور (ستاره ای که نور
از آن آمده) روی آن قرار داشته باشند. شکل زیر
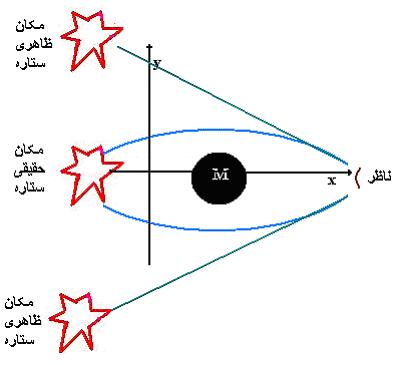
کنش
بار-رنگها و فوتون موجب تغییر مسیر پرتو نوری شده و
مسیر حرکت را خمیده می کند. اما بررسی تغییرات اندازه
ی حرکت روی محور افقی حاوی نکات بسیار ظریف و مهمی
است. زیرا این تغییرات می تواند جهت انتقال نور را
وارونه کرده و حتی موجب سقوط فوتون در جسم شود. به شکل
زیر توجه کنید:
نور در یک
میدان گرانشی شدید
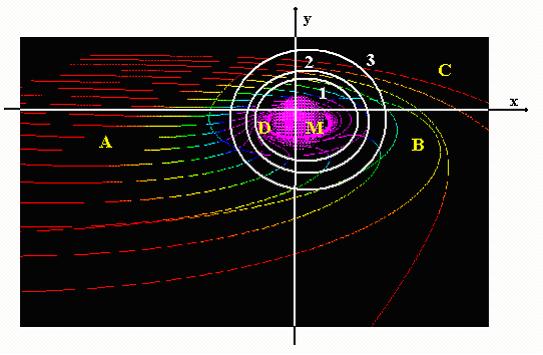
چند منطقه
در مسیر پرتو نوری در شکل انتخاب شده و بررسی می شوند.
A:
نور تقریباً
بطور عمودی بر سطح جسم حرکت میکند. اما جون بطور کامل
عمود نیست، بطور آزاد سقوط نمی کنند. اما جهت حرکت
آنها بگونه ای است که وارد سطح پتانسیل گرانشی 1 شده و
مانند سیاره ای بدور جسم بهDگردش
در می آیند. منطقه اندازه
حرکت و در نتیجه سرعتی که در جهت محور افقی x دارند،
مانع از سقوط کامل بدورن جسم است.
B: پرتوهایی
که در این منطقه حرکت می کنند، در سطح پتانسیل 1 و 2
در حرکتند، بعضی از این پرتوها (فوتونها) بسطح پتانیل
1 سقوط می کنند و بدور جسم می چرخند. اما برخی دیگر از
این پرتوها بر اثر تغییر اندازه ی حرکت افقی در جهت
مخالف حرکت اولیه برگشت داده شده و میدان گرانشی جسم
را ترک می کنند.
C: در
این منطقه تنها مسیر پرتوها تغییر می کند و میدان
گرانشی را ترک می کنند.
بطور کلی
آنچه که در اینجا حائز اهمیت است، توجه به اندازه حرکت
افقی فوتونهای فرودی و اندازه حرکت بار-رنگها است. به
شکل زیر توجه کنید:
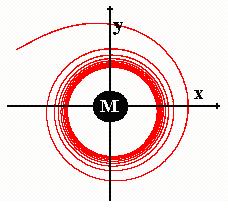
اندازه حرکت
فوتونها در جهت محور افقی تغییر می کند تا جاییکه به
مقدار ثابتی برسد
و سپس مانند
سیاره بدور جسم بگردش در می آیند.
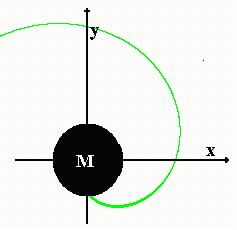
فوتون بسرعت
اندازه حرکت افقی و قائم خود را از دست می دهد و سقوط
می کند
محاسبه ی
انحنای فضا
یکبار دیگر
رابطه ی انحنای منحی را در نظر بگیرید:
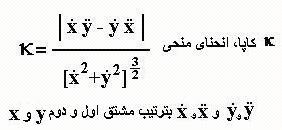
با توجه به
مطالب بخش قبل، حرکت پرتو نوری در میدان گرانشی روی هر
دو محور شتابدار است. بنابراین اگر شتاب روی دو محور
مشخص گردد، می توان با انتگرال گیری، سرعت را نیز به
دست آورد. همچنانکه در رابطه بالا مشخص شده، برای
محاسبه انحنای مسیر پرتو نوری به مشتق اول و دوم نیاز
داریم. مشتق اول سرعت و مشتق دوم شتاب است. لذا اگر
شتاب را داشته باشیم، در هر نقطه از مسیر می توان
انحنای مسیر نور را حساب کرد.
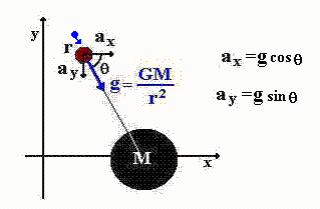
اما شتاب
تابعی سه نتغییره از فاصله، زاویه و زمان یعنی:(r, q
, t) است
که در روابط:

باید منظور
گردند. در حالیکه اگر از معادلات مربوط به اندازه ی
حرکت استفاده کنیم، بسیار زودتر و ساده تر به نتیجه
خواهیم رسید. زیرا در روابط:
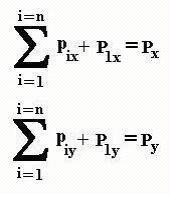
اگر شدت
میدان گرانشی را داشته باشیم (یا برای اجسام چگال فرض
کنیم) و با مقایسه آن با شدت میدان گرانشی اجسام
شناخته شده نظیر زمین، ماه و خورشید، می توانیم بخوبی
نتایج مورد نظر را به دست آوریم. تنها کافیست شدت
میدان گرانشی را با چگالی بار-رنگ در ارتباط قرار
دهیم. |

