|
نگاه اجمالی
از مکانیک
کلاسیک میدانیم
که در بررسی حرکت ذره ابتدا معادله
حرکت آن ذره
را پیدا میکنند و بر اساس آن در مورد چگونگی حرکت بحث میکنند. در
حالت کلاسیک ، بطور کلی این معادله با استفاده از لاگرانژین مربوط
به حرکت ذره حاصل میگردد. همچنین میدانیم که در مکانیک
کوانتومی ،
بر اساس نظریه
دوبروی در
مورد ذرات دو دیدگاه موجی و ذرهای در نظر گرفته میشود و اصل
مکملی نور مانع
از این میشود که این دو تصویر را به صورت همزمان بکار ببریم. ولی
برای توصیف کامل حرکت ، هر دو دیدگاه باید در نظر گرفته شوند. بر
این اساس معادلهای که به حرکت این ذرات کوانتومی حاکم است،
معادله شرودینگر نامیده میشود.
حرکت ذره آزاد
هر موجی که در جهت محور x انتشار
می یابد از معادله ی عمومی موج پیروی می کند که
در آن F تابع
موجی است که هم به مختصات x,
t بستگی
دارد و w سرعت
موج است. هنگامیکه امواج عرضی در امتداد یک تار کشیده منتشر می
شوند تابع F نمایشگر
تغییر مکان عرضی تار از حالت تعادل است و w سرعت
موج در امتداد تار است. وقتی امواج الکترومغناطیسی در خلا انتشار
می یابند F میدان
الکتریکی یا مغناطیسی و w سرعت
نور است. هنگامیکه امواج صوتی در یک گاز انتشار می یابند F,w به
ترتیب اختلاف فشار و سرعت صوت است.
در رفتار مکانیک موجی ذرات، تابع موج
کمیتی است که مجذور آن احتمال قرار گرفتن ذره را در هر نقطه ای از
فضا به دست می دهد که آن را با 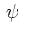 نشان
می دهند. نشان
می دهند.
معمولا سادهترین حالت در مکانیک
کوانتومی حرکت یک ذره
آزاد است. لفظ
آزاد به این لحاظ بکار میرود که این ذره تحت تاثیر هیچ پتانسیلی قرار
ندارد. در این صورت معادله شرودینگر در مورد حرکت ذره مورد نظر ،
با این فرض که حرکت در یک بعد صورت میگیرد، به صورت زیر خواهد بود:
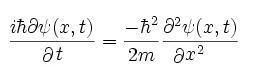
در رابطه فوق m جرم
ذره:
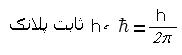
و:
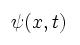
تابع موجی است
که در تشریح دیدگاه موجی ، به ذره مورد نظر نسبت داده میشود.
همچنین i یک
واحد موهومی است که مجذور آن برابر (1-) میباشد (عدد
مختلط). در این رابطه نماد:
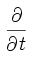
بیانگر مشتق
نسبی نسبت به
زمان و:
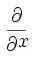
نشانگر مشتق نسبی
نسبت به مکان است.
خصوصیات معادله
شرودینگر
معادله شرودینگر
نسبت به مشتق زمان از مرتبه اول است. این امر ایجاب میکند که وقتی
مقدار اولیه تابع موج منتسب به ذره ، به عنوان مثال در لحظه t=0 معلوم
باشد، مقدار آن را در هر لحظه دیگر نیز بتوان پیدا کرد. این مطلب
از شکل این معادله ، یا از شکل عمومیترین جواب این معادله ، که یک
رابطه انتگرالی است، مشهود است.
نکته دیگر این
است که در معادله شرودینگر هیچ عدم
قطعیتی وجود
ندارد. به بیان دیگر ، همین که حالت اولیه تابع
موج مشخص شد،
در این صورت در هر زمان دیگری ، آن تابع موج کاملا مشخص میگردد.
دلیل این مطلب در اینجاست که هیچ محدودیتی بر روی تابع موج حالت
اولیه وجود ندارد.
چگالی احتمال
در حالت کلی تابع
موج 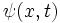 یک تابع
مختلط است و
به خودیخود هیچ تعبیر فیزیکی ندارد، اما مربع قدرمطلق آن کمیت
بسیار بااهمیتی است، که چگالی
احتمال نام
دارد. چگالی احتمال بیانگر احتمال وجود ذره است و در جایی که فرض
میشود، ذره در آنجا باشد، مقدار آن بزرگتر است و در هر جای دیگر
مقدار آن کوچکتر میباشد. چگالی احتمال که با یک تابع
مختلط است و
به خودیخود هیچ تعبیر فیزیکی ندارد، اما مربع قدرمطلق آن کمیت
بسیار بااهمیتی است، که چگالی
احتمال نام
دارد. چگالی احتمال بیانگر احتمال وجود ذره است و در جایی که فرض
میشود، ذره در آنجا باشد، مقدار آن بزرگتر است و در هر جای دیگر
مقدار آن کوچکتر میباشد. چگالی احتمال که با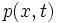 نمایش
داده میشود، یک تابع
حقیقی است و
وابستگی زمانی آن بیانگر این مطلب است که با گذشت زمان برای پیدا
کردن ذره در جایی که در لحظه اولیه قرار داشته، شانس کمتری وجود
دارد. نمایش
داده میشود، یک تابع
حقیقی است و
وابستگی زمانی آن بیانگر این مطلب است که با گذشت زمان برای پیدا
کردن ذره در جایی که در لحظه اولیه قرار داشته، شانس کمتری وجود
دارد.
معادله شرودینگر در
حالت کلی
در مطالب قبلی
معادله شرودینگر را در حالت ساده ذره آزاد و در مورد حرکت
یک بعدی بیان
کردیم. در صورتی که ذره مورد نظر آزاد نباشد، در این صورت تحت
تاثیر پتانسیلی مانند قرار خواهد داشت که در حالت تک بعدی پتانسیل
را با 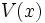 و
در حالت سه بعدی با و
در حالت سه بعدی با 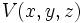 نشان
میدهیم و چون بیشتر پتانسیلهای مهم ، تقارن
کروی دارند،
لذا بهتر است که بحث را در مختصات
کروی انجام
دهیم. در این صورت پتانسیل به
صورت نشان
میدهیم و چون بیشتر پتانسیلهای مهم ، تقارن
کروی دارند،
لذا بهتر است که بحث را در مختصات
کروی انجام
دهیم. در این صورت پتانسیل به
صورت 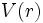 خواهد
بود. برای بیان معادله شرودینگر در حالت عمومی و در فضای
سه بعدی ،
تغییرات زیر را در معادله شرودینگر ذره آزاد اعمال میکنیم. خواهد
بود. برای بیان معادله شرودینگر در حالت عمومی و در فضای
سه بعدی ،
تغییرات زیر را در معادله شرودینگر ذره آزاد اعمال میکنیم.
تابع موج مربوط
به ذره را با 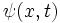 نمایش
میدهیم. نمایش
میدهیم.
مشتق نسبت به
مکان را در حالت سه بعدی با نماد 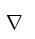 که
دل نامیده میشود، نشان میدهیم. که
دل نامیده میشود، نشان میدهیم.
چون ذره آزاد
نبوده و تحت تاثیر پتانسیل 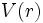 قرار
دارد، لذا یک جمله به صورت قرار
دارد، لذا یک جمله به صورت 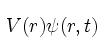 به
معادله اضافه میکنیم. بنابراین معادله شرودینگر در حالت کلی به
صورت زیر در میآید: به
معادله اضافه میکنیم. بنابراین معادله شرودینگر در حالت کلی به
صورت زیر در میآید:
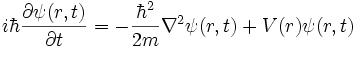
کاربرد معادله
شرودینگر
با استفاده از حل
معادله شرودینگر مشخصههای
سیستم از قبیل ترازهای
انرژی ، اندازه
حرکت خطی و اندازه
حرکت زاویهای سیستم
مشخص میشود.
از حل معادله شرودینگر تابع
موج منتسب به
هر سیستم فیزیکی بدست میآید. با استفاده از تابع موج میتوان چگالی
احتمال را
محاسبه نموده و حرکت ذرات سیستم را مورد بررسی قرار داد.
برای هر سیستم
معادله شرودینگر مخصوصی وجود دارد که وابسته به هامیلتونی تعریف
شده برای آن سیستم است.
نقل از رشد
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
آخرین
مقالات |

