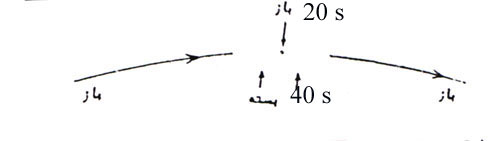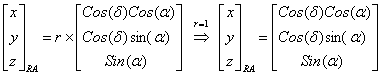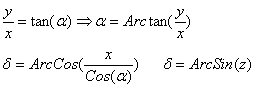نظریه سی پی اچ بر اساس تعمیم سرعت نور از انرژی به ماده بنا شده است.
سی پی اچ در ژورنالها
|
روشی دقيق برای آناليز عکسهای نجومی
|
||||
|
1- بررسی عکسهای نجومی اخذ شده جهت کشف اجسام سماوی جديد. 2- جهت تعيين موقعيت اجسام سماوی مانند دنباله دارها،نواخترهاو...... شرح مراحل کار : در گام اول نياز به گرفتن يک عکس نجومی از سوژه يا منطقه مورد نظر در آسمان داريم که شرايط عکسبرداری به صورت زير است: 1- مشاهدات برای عکس برداری از ستارگان بايد در شب صورت گيرد. 2- سوژه يا منطقه مورد نظر بايد از ماه بخصوص در هنگام کامل بودن ماه دور باشد تا به اطلاعاتی که لازم است بر روی آن ثبت شود خللی وارد نگردد. 3- بعلت وجود خطای انکسار (شکست نور)،منطقه يا سوژه مورد نظر نبايد در نزديکی افق قرار داشته باشد و بايستی که زمان عکسبرداری را طوری تنظيم کرد که سوژه در نزديکی افق نباشد. 4- بهيچ وجه از لنزهای wide برای عکسبرداری استفاده نشود و برای صحت هر چه بيشتر محاسبات بهتر است که از لنزهای تله استفاده شود. اصولا هرچه ميدان ديد کوچکتر باشد بهتر است. شيوه عکسبرداری نيز بشکل زير است : الف -ديافراگم عدسی شيئ بازميگردد. (هر جسم سماوی اثر پيوسته ای از خود باقی ميگذارد(برای مثال مدت 10 دقيقه عدسی شيئ باز باشد.)) ب -ديافراگم عدسی شيئ بمدت 40 ثانيه بسته ميگردد(ستاره اثری از خود بر روی عکس باقی نميگذارد.). ج -ديافراگم عدسی شيئ بمدت 10 تا 20 ثانيه باز می گردد(مدت باز ماندن مرتبط با محل سوژه در آسمان است.). د -ديافراگم عدسی شيئ بمدت 40 ثانيه بسته ميگردد (ستاره اثری از خود بر روی عکس باقی نمي گذارد.). ه -سپس دوباره ديافراگم عدسی باز ميگردد.(برای مثال همان مدت 10 دقيقه که در ابتدای کار داشتيم.). ردی که ستاره بر اثر اعمال اين 5 مرحله در هنگام عکسبرداری از خود بجا ميگذارد بشکل زير است :
علت استفاده از چنين ترفندی جهت عکسبرداری اين است که دقت لازم در چاپ عکسهای آنالوگ بخصوص در کشور ما صورت نمی گيردو شاهد نشستن گردوخاک و غيره بر روی عکس هستيم که در هنگام ظهور و چاپ بصورت لکه ها و نقاطی روشن بر روی عکس ثبت می شوند و ممکن است که بدليل شباهتشان با ستاره ها و يا ساير اجرام سماوی اشتباه گرفته شوند. برای جلوگيری از اين مسئله و بروز اين خطا لازم است که از روش فوق استفاده کنيم.در اينجا گام اول بپايان رسيد و يک عکس نجومي با شرايط لازم در اختيار شماست؛ حال بسراغ گام دوم می رويم :در اينجا دو فرض داريم؛ يکی اينکه در عکس مورد نظر جسمي سماوی وجود دارد که ما نياز به بررسی حرکت آن و در نتيجه محاسبه و بدست آوردن مختصات آن در روزهای مختلف داريم.برای مثال بررسی حرکت يک دنباله دار. فرض ديگر اين است که در عکس بدنبال کشف اجرام سماوی جديدی مانند دنباله دارها،نواخترها،ابرنواخترهاوغيره هستيم. چون تعداد ستارگانی که در يک عکس ثبت می شوند زياد است معمولا عکس را به شبکه های کوچکی تقسيم نموده وسپس تعداد ستاره ها در هر مربع يا مستطيل را شمرده و با نقشه مقايسه مي کنند.اما با روشي که در اين مقاله ذکر می شود می توان نشانه يک دستگاه را برروی هرجسم ثبت شده بر روی عکس برده و مختصات آن را با بدست آورده و با مقادير مختصات ستارگان موجود در آن ناحيه مقايسه کنيم.با اين روش ميتوان حرکت هاي بسيار اندک اجرام سماوی را نيز کنترل نمود. تعيين مختصات در اينجا هدف ماتعيين مختصات جسم يا اجسام ثبت شده مورد نظر بر روی عکسي است که به شيوه گفته شده در مرحله قبل تهيه کرده ايم.برای تعيين مختصات از روش يافتن مختصات تئوريک تقريبی و محاسبه شده و يا از دستگاهي بنام کمپاراتور(مونوکمپاراتور)می توانيم استفاده کنيم.روشی که در اينجا بکار برده مي شود و دارای دقتی در حد ميکرون است استفاده از دستگاهی با نام کمپاراتور است.کار اين دستگاه اندازه گيری بسيار دقيق(با تقريب ميکرون)مختصات قائم الزاويه نقاط مورد نظر بر روی عکس ميباشد.برای اندازه گيری های خيلی دقيق بر روی عکس ها در علوم فتوگرامتری(عکسبرداری هوايي) و ژئودزی فضايی (برای مثال ثبت ماهواره ها بر روی عکس و کنترل مختصات آنها) از دستگاهی بنام مقايسه گر (Comparator) استفاده می شود.کمپاراتورها بر دو نوعند : منو کمپاراتورها و استريو کمپاراتورها. از منو کمپاراتورها برای اندازه گيری بر روی يک عکس بهره گيری مي شود.کاربرد استريو کمپاراتورها در اندازه گيری فواصل بر روی يک زوج عکس مي باشد که در اينجا فقط روش کار با منو کمپاراتور را که به کار ما مربوط است توضيح داده می شود.
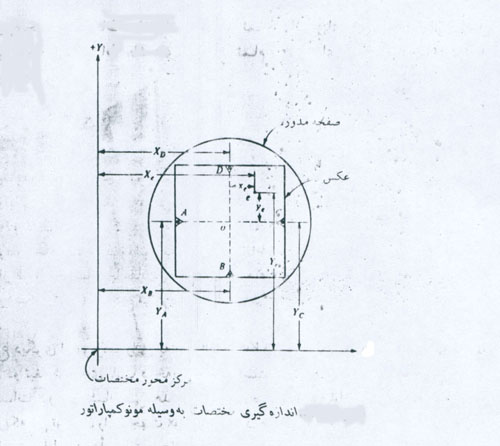
اين دستگاه قادر است فيلم های تا ابعاد 10 اينچی را بپذيردمضافا بر اينکه قادر است هم طول و هم زاويه را اندازه گيری نمايد. ابتدا فيلم يا دياپوزيتيو بر روی صفحه کمپاراتور قرار داده می شود.صفحه حامل فيلم در حول محور قائم قابل دوران بوده و دارای پنج حرکت کند مي باشد بطوريکه مي توان صفحه را با دقت 20 ثانيه قوسی دوران داد.با پيچی که در سمت راست دستگاه قرار دارد مي توان صفحه حامل فيلم را در جهت محور Xها حرکت داد.مشابه همين پيچ در سمت چپ دستگاه تعبيه شده که باعث حرکت صفحه در جهت محور Yها می گردد.پيچ ميکرومتر قادر است حرکت صفحه حامل فيلم را تا 001/0ميليمتر(1 ميکرون)نشان دهد.ميکروسکوپ چشمی با درشتنمايي 10 تا 20 برابر باعث تسريع در انطباق نشانه دستگاه روی نقاط مورد نظر می گردد. با دو روش مختصات عکسی نقاط بوسيله اين دستگاه اندازه گيری می شود. در روش اول عکس بطور دقيق روی صفحه نصب شده و صفحه را طوری دوران می دهند تا محور X عکس بر محور X دستگاه منطبق گردد.اين انطباق معمولا دارای خطاهايي است که بايد با استفاده از پيچ حرکت کند عمل را آنقدر تکرار نمود تا مختصات Y دو نقطه حاشيه عکس A و C که در شکل مشخص هستند کاملا شبيه هم شوند.پس از استقرار صفحه ، مختصات نقاط حاشيه عکس و ساير نقاط قرائت می شود.بدليل وجود خطاهای استقرار ، خطاهای قرائت منطبق نبودن محورهای عکس و کمپاراتور ، مختصات X نقاط حاشيه ای B و D با مختصات Y نقاط حاشيه ای A و C برابر نخواهند شد؛ به همين جهت مختصات xe وye نقطه e از تفاضل ميانگين مختصات Y نقاط حاشيه ای A وC از تمام قرائت های Y وهمچنين از تفاضل ميانگين مختصات Xنقاط حاشيه ای B وD ازتمام قرائت های X بدست خواه آمد. بعبارت ديگر : xe=Xe - ((XB+XD)/2) ye=Ye - ((YA+YC)/2)
*****************************************
روش دوم: اندازه گيری با منو کمپاراتورها موقعی نتيجه بهتری می دهد که ماشين حساب الکترونيکی موجود باشد.برعکس روش اول در اين روش انطباقی در مورد مختصات Y نقاط A و C صورت نمی گيرد بلکه بجای آن فيلم بحالت تقريب روی صفحه قرار داده می شودو مختصات نقاط حاشيه عکس و ساير نقاط اندازه گيری می گردد.سپس مختصات نقاط از طريق محاسباتي با مقايسه سيستم محورهای XY کمپاراتور و سيستم محورهای XY عکس تصحيح می گردد .يکي از روش های تصحيح، روش انتقال مختصات افاين است(Affine coordinate transformation) . البته بدليل پيچيده شدن بحث در باره اين روش و روش های مشابه آن صحبت نميشود ولی علاقه مندان مِتوانند برای مطالعه بيشتر به کتاب PHOTOGRAMMETRY نوشته MOFFITT و MIKHAIL (به زبان اصلي است.) و يا به کتاب مباني فتوگرامتری نوشته دکتر مجيد همراه مراجعه کنند. لازم بذکر است که مي توان به کمپاراتورها encoder متصل کرد تا بتوان قرائت ها را بطور بطور عددی و ديجيتالی وارد رايانه نمود.اگر تعداد اندازه گيری ها زياد باشد واضح است که encoder باعث حذف مقداری از خطاهای انسانی گرديده و محاسبات ما را سرعت می بخشد(استفاده از encoder روش بسيار مناسبي است و استفاده از آن توصيه ميشود.) . البته بر روی مقادير بدست آمده از روش کمپاراتور ميتوان تصحِحات زيادی رااعمال کردمن جمله خطاهای سيستماتيکی مانند عدم انطباق محورهای عکسی با نقطه اصلی ، تغيير بعد عکس ، خطای عدسی ، خطای انکسار اتمسفر ، خطای کرويت زمين. ولی بدليل اينکه بدون وارد کردن تصحيحات فوق الذکر هم مقادير بدست آمده نياز ما را بخوبي تامين مي کنند از دخالت دادن اين تصحيحات در اندازه گيری هاي مان صرفنظر ميکنيم.حال فرض می کنيم که مختصات قائم الزاويه سوژه يا سوژه های مورد نظر بر روی عکس را توسط کمپاراتور بدست آورده ايم.اين مختصات و موقعيت نسبت به يک محور X و Y که مبداشان مرکز عکس است بدست آمده است.(مرکز عکس را ميتوان از محل تقاطع دو وتر عکس معين کرد.)ولی مختصاتي که ما از ستارگان در کتب و منابع مختلف در دست داريم نسبت به مرکز کره سماوی سنجيده ميشود.حال ما نياز به روابطی داريم که از طريق آنها بتوانيم اين مختصاتها را بيکديگر تبديل کنيم.در اينجا ما از تبديلات ماتريسي استفاده ميکنيم يعني ابتدا مختصات منحنی الخط (بعد و ميل )هر ستاره را تبديل به مختصات مستقيم الخط (X وY وZ ) می نماييم.سپس مختصات X وYوZ اجسام سماوی مورد نظر را که نسبت به مرکز کره سماوی است به X وYو Z تحت سيستم مختصات عکس وبالعکس تبديل می کنيم. (مولفه Z در عمل برابر صفر می باشد چون محدوده عکس آنچنان بزرگ نيست که عکس را يک صفحه منحني در نظر بگيريم.البته شرط لازم برای محقق شدن اين حالت اينست که از لنزهای تله استفاده شود .اصولا ميدان ديد دوربين هر چه کمتر باشد محاسبات از صحت بيشتری برخوردارست چرا که منطقه عکسبرداری هر چه کوچکتر باشد از انحنای آن کاسته شده و به سطح تخت نزديکتر ميشود.)
حال تبديلات لازم را مرحله به مرحله ذکر می کنيم.(دراينجا ما مختصات تمام ستارگان را از بعد و ميل به مختصات عکسی تبديل می کنيم.) 1- تبديل مختصات منحنی الخط سوژه موردنظر ( بعد a وميل dمرکز عکس) به مختصات مستقيم الخط(X وY وZ )
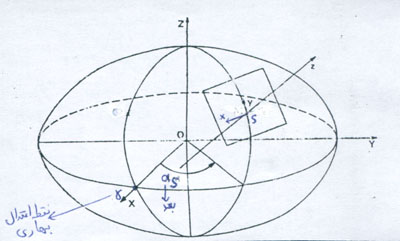
r= شعاع کره سماوی که برابر با مقدار واحد (1) است. در مرحله بعد مبداء مختصات را ا ز مرکز کره سماوی به نقطه ای بر روی سطح کره سماوی انتقال ميدهيم.(در شکل اين تبديل بخوبی نشان داده شده است.)
روابط مربوط به اين انتقال مختصات به شرح زير است :
rs = es چون مقدار شعاع کره سماوی 1 در نظر گرفته می شود
مشخصات سيستم O : مبداء= مرکز کره سماوی محور Z = در راستای محور کره سماوی که از قطب شمال و جنوب سماوی ميگذرد بسمت بالا. محور X= امتداد آن از نقطه اعتدال بهاری می گذرد. محور Y= سيستم را راستگرد می سازد.
مشخصات سيستم S : مبداء= نقطه ای فرضی بر روی سطح کره سماوی محور Y = امتداد آن از شمال نجومی ميگذرد. محور X = سيستم را چپگرد ميسازد. البته مسئله ای که در اين ميان مطرح می شود وجود مولفه Z برای هر نقطه است .بدليل اينکه تمامي نقاط ما بر روی صفحه ای با انحنای کم قرار دارند در نتيجه Z تمام نقاط باهم برابر فرض ميشود.(هرچقدرانحنای اين صفحه کمتر شود يعنی بعبارت ديگر ميدان ديد عدسی شئ وسيله عکسبرداری کوچکتر باشد اين تقريب از دقت بالاتری برخوردار خواهد شد.)علت برابر دانستن Z نقاط اينست که COMPARATOR تنها قادر به اندازه گيری موقعيت در سيستم مختصات دوبعدی می باشد و قادر به اندازه گيری مولفه Z نيست.البته از طريق محاسبات براحتی ميتوان تصحيحات را به Z نقاط وارد نمود و از دقت بسيار بالا استفاده نمود.برای اينکار مي بايست ازفرمولهای هندسه کروی استفاده نمود .مختصات Xo وYo وZo ستارگان را ميتوان از کتاب APFS )Apparant Place of Fundamential Stars) که هر ساله چاپ ميشود و يا نرم افزارهای نجومی معتبر استخراج نمود.همچنين نياز نيست مراحل ذکر شده در بالا را هر بار بطور دستی ويا با ماشين حساب برای هرجسم سماوی محاسبه کنيم؛ بلکه ميتوان برنامه ای کوتاه برای مثال توسط نرم افزار MATLAB نوشت که در ورودی بعد و ميل يا X وY وZ ستارگان را دريافت کرده و XوYوZ آنها در سيستم مختصات برای مثال S رادر خروجی بما بدهد.در نتيجه براحتی ميتوان مختصات ستارگان را با کمپاراتور در يک سيستم مختصات قائرم الزاويه نسبت به مرکز عکس بدست آورده وبا مختصات های بدست آمده از روش قبل مقايسه نمود. البته ميتوان به شيوه ديگری هم عمل نمود ؛ يعنی پس از بدست آوردن مختصات هر جسم سماوی مختصات آن را به سيستم مختصات O با مبداء کره سماوی انتقال داد . برای مثال اگر بخواهيم X وY وZ بدست آمده در سيستم O را بهd وa
با استفاده از فرمول های ذکر شده در اين مفاله می توان مختصات تمامی اجرام ثبت شده بر روی يک عکس را کنترل نموده و يا مختصات اجسام مورد نظر را با دقت بسيار خوبی بدست آورد.البته در تمامی محاسبات بعد از اينکهX وY را با کمپاراتور محاسبه نموديم به Zمقدار صفر را بايد اختصاص دهيم .روشی که در بالا گفته شد برای عکسهای آنالوگ ميباشد.مي توان برنامه ای رايانه ای نوشت که به عکس يک سيستم مختصات اختصاص دهد و تمام اين مراحل را بصورت يک نرم افزار انجام دهد.مسلما تلاش و زمان زيادی را مي طلبد اما در صورت تحقق اين امر استفاده های فراوانی از آن خواهد شد.در پايان ذکر اين نکته لازم است که مطالب مندرج در اين مقاله به صورت گسترده انجام نشده و تنها در گذشته در ژئودزی فضايي برای بدست آوردن مختصات ماهواره ها بشکلی مشابه با روش گفته شده در اين مقاله از کمپاراتور استفاده می شده است که البته شکل و روش انجام کار و محاسبات با آنچه در اين مقاله آمده است متفاوت باشد.اميد آنکه اين مقاله برای تمامی خوانندگان آن مفيد واقع گردد.
منبع : انجمن علمي پژوهشي نجم شمال نویسنده : سيد مازيار سيدنژاد
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
|
Sub quantum space and interactions from photon to fermions and bosons |
آرشیو موضوعی

از آغاز کودکی به پدیده های فیزیکی و قوانین حاکم بر جهان هستی کنجکاو بودم. از همان زمان دو کمیت زمان و انرژی بیش از همه برایم مبهم بود. می خواستم بدانم ماهیت زمان چیست و ماهیت انرژی چیست؟