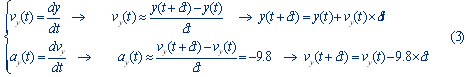|
شبيهسازي حركت سقوط آزاد
آنچه از اين بحث ميآموزيم:
1. تقريب
عددي مرتبة اول مشتق.
2. آشنايي با
گام زماني.
3. آشنايي با
حلقههاي برنامهنويسي و اهميت آنها.
ميخواهيم يك حركت
سقوط آزاد را مدل و شبيه سازي كنيم (اين مسئله يك مسئلة اتمي
ملكولي نيست):
1. تمام روابط
رياضي آن موجود است، ولي ما نميخواهيم با دانستن جواب ــ يعني
فرمولهاي حركت سقوط آزاد ــ به حل مسئله بپردازيم. (هر چند آنهم
در جاي خود آموزنده است.)
2. در شبيه سازي فرض ميشود که ما فقط قوانين اصلي را داريم (اينجا
قانون دوم نيوتن). همينطور اثر دنياي خارج از يك سيستم (گلوله
در حال سقوط) را بر آن به صورت نيروهاي معروف (اينجا نيروي
جاذبة زمين) ميشناسيم. بعد به حل عددي معادلة نيوتن در
كامپيوتر ميپردازيم (بعداً بيشتر در اين باره صحبت خواهيم کرد).
شايد سؤال شود اگر ما جواب را داريم پس دنبال چه چيزي هستيم؟
بايد گفت كه ما با طرح مسائلي كه از قبل حل شدهاند، توان عملي
خود را در پيشگوييهاي ازقبلمشخص محك ميزنيم تا در آينده به
حل مسائل حلنشده بپردازيم.
3. با شروع از يك سري اعداد و ارقام اوليه ــ كه به شرايط
اولية مسئله وابستهاند ــ آيندة سيستم را به كمك حلهاي عددي
معادلة نيوتن پيشبيني كنيم و اگر موضوع يك ذرة مادي است مسير
آن را ردگيري نماييم و تمام خصوصيات مورد نياز را محاسبه كنيم.
4. در مرحلة بعدي به كمك قانون دوم كه مناسب حركتهاي معمولي
است، به رديابي ذره به كمك كدهاي كامپيوتري بپردازيم. اين روش
ردگيري را «ديناميك مولكولي» ميگويند.
همچنين روش عملياتي يا پياده كردن اين مدلها را به صورت
رياضي، «آناليز عددي» يا «حل عددي كامپيوتري» ميگويند.
براي آنكه با
نمونهاي از «حلّ عددي» آشنا شويد، به حلّ عددي معادلات (يا
مشتقات) سادة 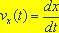 و و 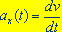 در
تقريب در
تقريب
اول به كمك تعريف
مشتق تابع (مشتق يك تابع در واقع شيب يك تابع در نقطة دلخواه است)
ميپردازيم. مثلاً اگر تابع Y(t) را
در
دستگاه y- t رسم
كنيم، شيب خط مماس در نقطة 1 t
برابر 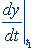 است.
توجّه كنيد: است.
توجّه كنيد:
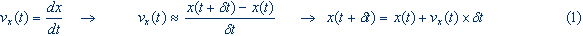
در يك
شبيهسازي از t=0 در رابطة 1 شروع ميكنيم. بعد با در نظر گرفتن
مقداري براي كه «گام
زماني» ناميده
ميشود (انتخاب مقدار گام زماني بسيار كليدي است) به مقدار x در
زمانهاي بعدي ميرسيم. سرعت ذره در گام بعدي را هم با كمك
رابطهاي مشابه با حلّ عددي معادلة دوم به دست ميآوريم:
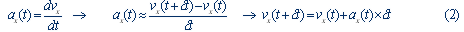
براي يك حركت
شتابدار ثابت مقدار a در رابطة اخير مشخص است.
رابطههاي 1و2 حلّ عددي معادلات مذكور هستند (كه به روش اويلر
معروف است). بعداً بهتفصيل به روشهاي بادقتِ بيشتر باز خواهيم
گشت.
در مثال سقوط آزاد، به جاي a عدد 8/9- (شتاب گرانش) را ميگذاريم و
چون حركت در راستاي قائم است از y به جاي x استفاده ميكنيم:
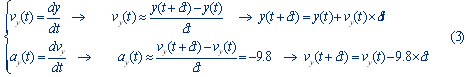
بهتر است اين
معادلات را براي راحتي كار به صورت زير بازنويسي كنيم:

انديس i نشاندهندة
تعداد گامهاست. رابطة 4 سادهترين نوع از الگوريتمهاي حل قانون
دوم نيوتن است.
شرايط اولية سقوط ــ
سرعت و محل اوليه ــ را
مينويسيم:

در جدول زير(كه تنها
چند مقدار اول از نتايج محاسبات آمده است) با توجه به رابطه 4 براي
محل ذرات و انتخاب گامهاي زماني 01/ 0 و 05/0، تعدادي از yها توليد
شده اند. به عبارت ديگر تابع Y(t) به
صورت گسسته- يعني يكسري عدد- پيدا مي شود.
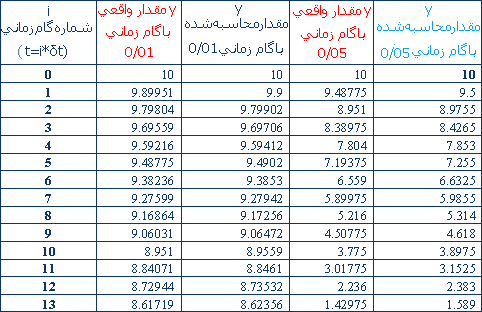
اين اعداد محلّ ذرّه
را در لحظات مختلف نشان ميدهند.
اكنون ميتوان تابع گسسته محاسبه شده با گام 005/0 را با جواب
واقعي ــ كه يك سهمي است و به صورت خط چين نشان داده شده است. ــ
مقايسه كرد.

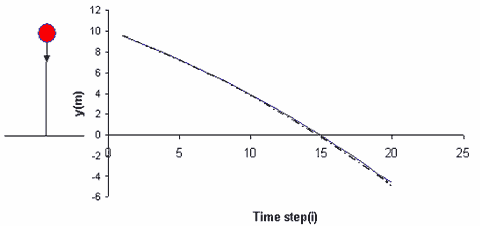
شکل 2: مقايسه جواب به دست آمده از حل عددي و جواب واقعي براي
مساله سقوط آزاد
دكمهاي روي فرم
استاندارد ويژوال بيسيك طراحي كنيد و سپس داخل آن برنامة زير را
بنويسيد:
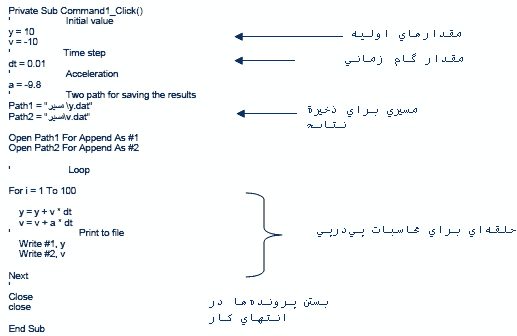
(در زبانهاي
برنامه نويسي براي انجام عمليات تكراري از ساختار حلقه استفاده مي
شود).
پس از اجراي برنامه، دو فايل يكي حاوي مكان ذرات (y.dat) و ديگري
سرعت آنها (v.dat) در مسير مدّ نظر ساخته مي شود. اگر اين برنامه
را براي گام 01/0 نيز اجرا كنيم، جوابهاي y را نسبت به شماره گام
زماني مطابق جدول بالا تعيين ميشوند. كم كردن گام زماني از 05/0 به
01/0 نتيجه را هر چند بهبود بخشيده است (اعداد ستونهاي مربوط به يك
گام زماني را باهم مقايسه كنيد.)، ولي تحول سيستم آرام آرام صورت
مي گيرد و پيشروي الگوريتم بسيار كند ميشود، يعني گلوله براي رسيدن
به زمين تعداد گامهاي بيشتري نياز دارد. اينجاست كه اهميّت گام
زماني از دو نظر سرعت و دقّت در شبيه سازيها مشخّص مي شود. همينطور
دقت كنيم كه زمان حل مساله توسط كامپيوتر وابسته به تعداد گامهاي
زماني است بنابراين الگوريتمي مفيد است كه تعداد گامهاي زمانيش در
عين دقيق بودن نتايج مناسب باشد و سر به فلك نكشد!
تمرين
1. نرمافزار ويژوالبيسيك را نصب و كمي با آن كار كنيد. (با يك
ساعت مطالعه، به هدف اين فصل خواهيد رسيد).
2. نتايج مندرج در جدول و نمودار بالا را به دست آوريد.
3. با توجه به معادلات 1و2 علت اهميت مقدار گام زماني را توضيح
دهيد.
4. نموداري براي گام زماني 005/0 ترسيم و با جواب واقعي مقايسه
كنيد.
5. نموداري براي سرعت محاسبهشده ترسيم و با نمودار جواب واقعي كه
يك خط است در يك صفحه ترسيم كنيد. در مورد سرعت خواهيم ديد كه خطا
صفر است و با انتخاب هر گام زماني جوابمان دقيق خواهد بود. چرا؟
6. آيا ميتوان گفت گام زماني 0005/0 به جواب واقعي نزديكتر است؟
چرا؟
7. الگوريتمهاي
ديگري نيز براي حل معادلات 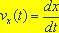 و و 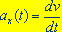 مثل
اويلر ـ ريچاردسون، ورله و رانگ ـ كوتا وجود دارند كه مثل
اويلر ـ ريچاردسون، ورله و رانگ ـ كوتا وجود دارند كه
دقت محاسبات
را به علت استفاده از مراتب بالاتر افزايش ميدهند. دربارة
الگوريتمهاي ديگر تحقيق كنيد.
برنامهاي ساده براي بررسي عددي اين مساله در اختيار شما قرار
گرفته است: برنامه
سقوط آزاد
--- كد
برنامه سقوط آزاد
در كنار فايل اجرايي كدهاي برنامه به زبان ويزوال بيسيك نيز براي
بچههايي كه با برنامه نويسي ميانه خوبي دارند، گذاشته شده است.
منبع: باشگاه
نانو
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
آخرین
مقالات |