|
Pick Four: Gravity, Quantum, Length, Width, Depth
By Johannes
Koelman |
April 8th 201
In my late teenage years I grew fond of Scientific American.
Although language caused a barrier, and while I could digest and
understand only some of the articles, the popscience presented
opened my eyes to exciting developments and invited me to study
further the subjects presented.
These days, many years later, I still glance through the
magazine, but generally with less enthusiasm. Today's editions
seem packed with rather superficial information, and the
articles tend to be less inviting towards further studies. Yet,
once in a while, a hidden jewel attracts my attention. Such is
the case this month with an article by Steve Carlip from UC
Davis. Subject is quantum gravity. Quantum gravity in a pancake
universe, that is.
The article makes frequent reference to Edwin Abbott's 1884
novel "Flatland,
A Romance of Many Dimensions" and
is aptly entitled "Quantum
Gravity in Flatland".
Carlip eloquently explains why the holy grail of modern physics,
the unification of gravity and quantum mechanics, is much less
problematic when one sacrifices one spatial dimension. The key
theoretical observation is that in contrast to what is the case
in our 3D universe, in Flatland there is no opportunity for
gravitational fields to propagate. There are no gravitational
waves and therefore no gravitons. This means that Flatland lacks
the gravitational degrees of freedom that cause quantum gravity
calculations to blow up. Without such degrees of freedom,
quantum gravity theory is straightforward, and the math provides
sensible answers.
However, the absence of gravitational degrees of freedom not
only renders quantum gravity in Flatland mathematically
tractable, it also renders it empty. In simple terms: without
gravitational degrees of freedom there is not much left to be
quantized. After some initial explorations, quantum gravity
theorists therefore started to consider Flatland a barren land.
Interest in 2D quantum gravity faded, and the subject no long
attracted much attention.
This all changed in 1989 when Ed Witten pointed out that
Flatland is less barren than everyone assumed. Although void of
local gravitational degrees of freedom, 2D planar space can
accommodate global gravitational degrees of freedom. These
degrees of freedom are topological in nature, and the trick
therefore is to allow topologically more interesting Flatlands.
In his Scientific American article, Carlip discusses what is
probably the easiest realization of topological gravity: a
spatially flat 2D universe with the topology of a donut surface.
Such a donut topology is defined by the fact that you can return
to your original position via two distinct routes neither of
which can be shrunk to zero size, and that can not be morphed
into each other. A donut accommodates such alternate routes:
those that go around via the central hole, and those that go
around the rim. A donut achieves these topological
characteristics at the expense of bending its surface. However,
the very same topology can be achieved for a perfectly flat
surface. All that is required is an unlimited number of copies
of a flat piece that can be connected together in a periodic
fashion and without leaving any gaps. Below figure gives an
example of such a periodic universe with one particular return
route rendered visible.

So how does gravity manifest itself in such a Donuverse? As
shown in below animation, the Donuverse morphs from a degenerate
initial state into a planiverse and back into a degenerate
state. In other words, the Donuverse is periodic not only in
space but also in time. The degenerate state corresponds to the
big bang, or rather the big bounce as it marks both the start
and the end of the universe.
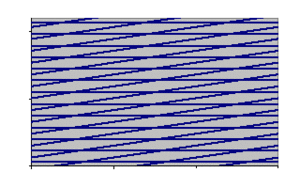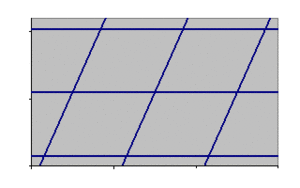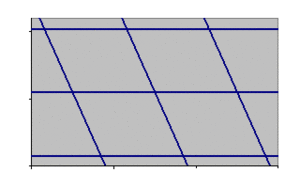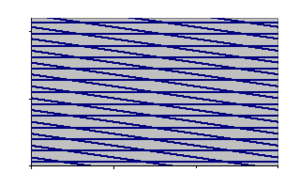
This model universe is certainly not an accurate model of our
universe, not only because it lacks a third spatial dimension,
but also because it fails to exhibit accelerated expansion. Yet
it is a model that can be quantized, and as such it provides an
interesting playground for theorists. Playing with such toy
models, in 1992 three Chilean theorists, Banados, Teitelboim and
Zanelli, made the amazing discovery that two spatial dimensions
are sufficient to accommodate black holes. All that is needed to
render possible black holes in Flatland is the addition of some
negative vacuum energy. Although of lower dimension, the
resulting BTZ black holes are just like the black holes that are
believed to populate our universe. More in particular, BTZ holes
have a temperature and radiate just as predicted by Hawking.
This seems most puzzling. In the absence of local degrees of
freedom, how can a Flatland black hole have a temperature and
radiate?
A quantum gravitational study of BTZ black revealed that
although a 2D universe is like a sea without waves, when it
incorporates islands (black holes), these are surrounded by a
surf. In other words: the edges of Flatland vibrate and wiggle.
And they do so in a way that yields a temperature exactly as
predicted by Hawking. This provides us with what seems to be a
remarkable realization of a holographic universe. In this case
the universe is two-dimensional with the degrees of freedom
residing at one-dimensional boundaries.
Rather than a barren landscape, Flatland has proved to be a most
interesting area to explore. The hope is that Flatland models
will provide a testbed to elucidate fundamental concepts of
quantum gravity such as the nature of holographic degrees of
freedom. But there are limitations to what Flatland models can
teach us. As stated before, an important limitation of Flatland
quantum gravity is that is void of local degrees of freedom. One
therefore may question whether Flatland models will be
sufficiently rich to clarify the unknown holographic
relationship that many researchers believe to provide a link
between local degrees of freedom and those at the 'edges' of the
universe.
Recent work by
Witten (again!) and Maloney suggests that Flatland quantum
gravity is a subject still far from being fully understood.
Either Flatland gravity models are too restrictive to help us
understand real world gravity, or gravity is a phenomenon even
more subtle than we so far have assume it to be. In the latter
case we will desperately need Flatland models to sharpen our
intuition and to get ready for the real thing: quantum-gravity
theory in Spaceland.
In any case, as is often the case, Einstein has the last word.
That also holds true for the subject of simplified quantum
gravity models:

--------------
Not afraid of some math, and want to read more about planar
black holes and Donuverses? Checkthis
overview article by
Steve Carlip.
Source: Science
2.0
1 2 3 4 5 6 7 8 9 10 Newest
articles
|




