CPH Theory

In recent posts we’ve seen how the Higgs gives a mass to matter particles and force particles. While this is nice, it is hardly a requirement there must be a Higgs boson—maybe particles just happen to have mass and there’s no “deeper” origin of that mass. In fact, there’s a different reason why particle physicists are obsessed about finding the Higgs (or something like it)—that’s called electroweak symmetry breaking.

That’s pretty heady stuff, but we’ll take it one piece at a time. Write it down and use it to impress your friends. Just be sure that you read the rest of this post so you can explain it to them afterward. (There’s a second part to the statement that we’ll examine in a follow up post.)

You might be familiar with the idea that electricity and magnetism are two manifestations of the same fundamental force. This is manifested in Maxwell’s equations and is often seen written on t-shirts worn by physics undergraduates. (If you happen to own such a t-shirt, I refer you to this article.) Electroweak symmetry is, in a sense, the next step in this progression, by which the electromagnetic force is unified with the weak force. This unification into an ‘electroweak’ theory and the theory’s subsequent ‘breaking’ into separate electromagnetic and weak forces led to the 1979 Nobel Prize in Physics.

So what’s going on here? We know that the force particle for electromagnetism is the photon, and we know that the force particles for the weak force are the W+, W-, and Z bosons. Permit me to make the a priori bold claim that the “unified” set of particles are actually the following: three W bosons and something we’ll call a B boson.

What? Now there are three W particles? And what’s this funny B boson; we never drew any diagrams with that weirdo in our guide to Feynman diagrams! Don’t worry, we’ll see shortly that because of the Higgs, these particles all mix up into the usual gauge bosons that we know and love. This should at least be plausible, since there are four particles above which we know must give us the four electroweak particles that we know: the W+, W-, photon, and Z.

Note that this new “unified” batch of gauge bosons don’t really look very unified: The Ws look completely different from the B. This illustration reflects an actual physical difference: the Ws mediate one type of force while the B mediates a different force. In this sense, the “unified” electroweak symmetry isn’t actually so unified!

ELECTROWEAK SYMMETRY IS BROKEN

In everyday phenomena, we observe electricity and magnetism as distinct phenomena. The same thing happens for electromagnetism and the weak force: instead of seeing three massless Ws and a masslessB, we see two massive charged weak bosons (W+ and W-), a massive neutral weak boson (Z) and a massless photon. We say that electroweak symmetry is broken down to electromagnetism.

Now that masses have come up you should suspect that the Higgs has something to do with this. Now is a good time to remember that there are, in fact, four Higgs bosons: three of which are “eaten” by the weak gauge bosons to allow them to become massive. It turns out that this “eating” does more that that: it combines the ‘unified’ electroweak bosons into their ‘not-unified’ combinations!

The first two are easy; the W1 and W2 combine into the W+ and W- by “eating” the charged Higgs bosons. (Technically we should now call them “Goldstone” bosons.)

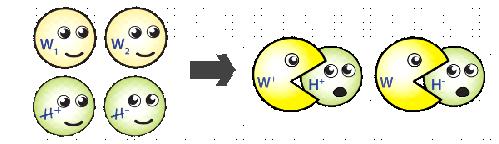
We’ll say a bit more about why eating a Higgs/Goldstone can cause the W1 and W2 particles to combine into, say, a W+. For now, note that the number of “degrees of freedom” match. Recall that ‘degree of freedom’ roughly translates in to the number of distinct particle states. In the electroweak theory we have two massless gauge bosons (2 × 2 polarizations = 4 degrees of freedom) and two charged Higgses (2 degrees of freedom) for a total of six degrees of freedom. In the broken theory, we have two massive gauge bosons (2 × 3 polarizations) which again total to six degrees of freedom.

A similar story goes through for the W3, B, and H⁰ (recall that this is not the same as the Higgs boson, which we write with a lowercase h). The W3 and B combine and eat the neutral Higgs/Goldstone to form the massive Z boson. Meanwhile, the photon is the leftover combination of the W3 and B. There are no more Higgses to eat, so the photon remains massless.

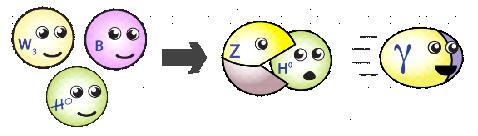
It’s worth noting that the Ws didn’t combine into charged Ws until electroweak symmetry breaking. This is because [electric] charge isn’t even well-defined until the electroweak theory has broken to electromagnetic theory. It’s only after this breaking that we have a photon that mediates the force that defines electric charge.

ELECTROWEAK SYMMETRY IS BROKEN SPONTANEOUSLY

Alright, we have some sense of what it means that “electroweak symmetry” is broken. What does it mean that it’s broken spontaneously, and what does this whole story have to do with the Higgs? Now we start getting into the thick of things.

The punchline is this: the Higgs vacuum expectation value (“vev” for short) is what breaks electroweak symmetry. You might want t quickly review this post where we first introduced the Higgs vev in the context of particle mass. For those who like hearing fancy physics-jargon, you can use the following line:

First, let’s see why the Higgs obtains a vacuum expectation value at all. We can draw nice pictures since the vev is a classical quantity. The potential is a function that tells you the energy of a particular configuration. You might recall problems in high school physics where you had to find the minimum of an electric potential, or determine the gravitation potential energy of a rock being held at some height. This is pretty much the same thing: we would like to draw the potential of the Higgs field. (To be technically clear: this is the potential for the combined bunch of four Higgses.)

Let’s start with what a “normal” potential looks like. Here on the x and y axes we’ve plotted the real and imaginary parts of a field ϕ; all that’s important is that a point on the x-y plane corresponds to a particular field configuration. If the particle is sitting at the origin (in the middle) then it has no vacuum expectation value, otherwise, it does obtain a vacuum expectation value.

On the z axis we draw the potential V(ϕ). The particle wants to roll to the minimum of the potential, so in the cartoon above—the “normal” case—the particle obtains no vacuum expectation value. I’ll mention in passing that concave of the potential is related to the particle’s mass.

Now let’s examine what the Higgs potential looks like. Physicists refer to this as the “Mexican hat” potential (These images are based on an illustration that is often used in physics talks. Unfortunately I am unable to find the original source of this graphic and ended up re-drawing it.):

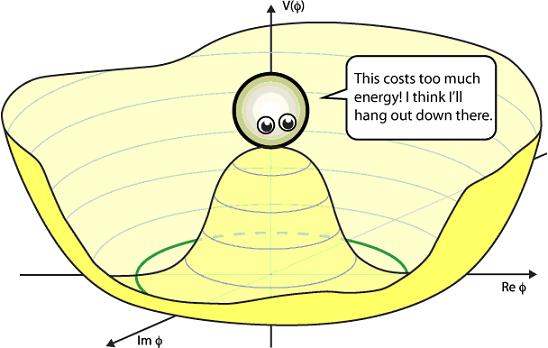
What we observe is that the origin is no longer a minimum of the potential. In other words, the Higgs wants to roll down the hill where it can have lower potential energy. I’m not telling you why the potential is shaped this way (there are a few plausible guesses), and within the Standard Model this is an assumption about the Higgs.

So the Higgs must roll off of its hill into the ravine of minimum potential energy. This happens at every point in spacetime, meaning that the Higgs vev is “on” everywhere and matter particles can bounce off it to obtain mass. There’s something even more important though: this vev breaks electroweak symmetry.

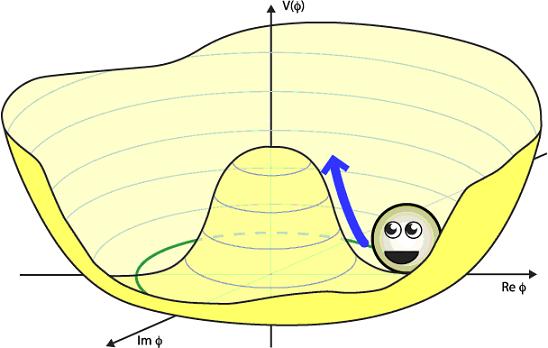
In the cartoons above, there’s something special about the origin. If the particle sits at the origin, you can do a rotation about the x-y plane and the configuration doesn’t change. On the other hand, if the particle is off of the origin, then doing a rotation will send the particle around along a circular trajectory (shown as a solid green line). In other words, the rotational symmetry is broken because the physical configuration changes.

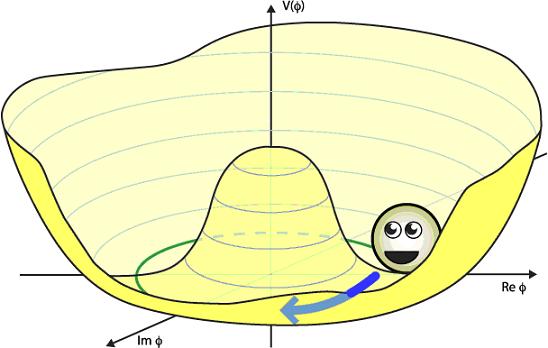
The case of electroweak symmetry is the same, though it requires more dimensions than we can comfortably draw. The point is that there are originally four Higgses which are all parts of a single “Higgs.” In the unified theory where electroweak symmetry is unbroken, these four Higgses can be rotated into one another and the physics doesn’t change. However, when we include the Mexican hat potential, the system rolls into the bottom of the Mexican hat: one of the Higgses obtains a vev while the others do not. Performing a “rotation” then moves the vev from one Higgs to the others and the symmetry is broken—the four Higgses are no longer being treated equally.

Now to whet your appetite for my next post: you can see that once electroweak symmetry is broken, there is a “flat direction” in the potential (the green circle). Remember when I said that the concave of the potential has to do with the particle’s mass? The fact that there is a flat direction means that there are massless particles. In fact, for the Higgs, there are three flat directions that correspond to—you guessed it—the three massless Higgs/Goldstone particles which are eaten by the weak gauge bosons: the H+, H-, and H⁰. The fourth Higgs—the particle that we usually call the Higgs—corresponds to an excitation in the radial direction where there is a concave, so the Higgs boson has mass.

DO WE REALLY NEED A HIGGS?

Okay, so if you’ve followed so far, you have an idea of how electroweak symmetry breaking explains how the massless W and B bosons combine with the Higgses to form the usual W+, W-, Z, and photon. We’ve also reviewed how matter particles get mass (by bumping into the resulting vev) and how some of those gauge bosons got mass (by eating some of the Higgses). But was all of this necessary, or did we just cook it all up because we liked the idea of electroweak unification?

We will see in one of my follow up posts that in fact, electroweak symmetry breaking is almost necessary for our theory to make sense. (I’ll quantify the “almost” when we get there, but the technical phrase will be “perturbative unitarity.”) Note that I said that electroweak symmetry breaking is the important thing. Throughout this entire post you could have replaced the Higgs boson with “something like it.” There are plenty of theories out there with multiple Higgs bosons, no Higgs bosons, or generically Higgsy-things-but-not-quite-the-Higgs. That’s fine—in all of these theories, the “Higgsy-thing” always breaks electroweak symmetry. In doing so, you always end up with Goldstone bosons that are eaten by the W+, W-, and Z. And you always end up with some kind of particle like the Higgs that we expect to find at the LHC.

Why do we expect a Higgs boson? Part II: Unitarization of Vector Boson Scattering

Hi everyone—it’s time that I wrap up some old posts about the Higgs boson. Last December’s tantalizing results may end up being the first signals of the real deal and the physics community is eagerly awaiting the combined results to be announce at the Rencontres de Moriond conference next month. So now would be a great time to remind ourselves of why we’re making such a big deal out of the Higgs.

Review of the story so far

Since it’s been a while since I’ve posted (sorry about that!), let’s review the main points that we’ve developed so far. See the linked posts for a reminder of the ideas behind the words and pictures.

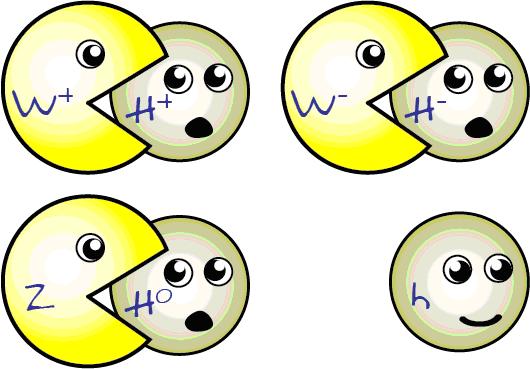
There’s not only one, but four particles associated with the Higgs. Three of these particles “eaten” by the Wand Z bosons to become massive; they form the “longitudinal polarization” of those massive particles. The fourth particle—the one we really mean when we refer to The Higgs boson—is responsible forelectroweak symmetry breaking. A cartoon picture would look something like this:

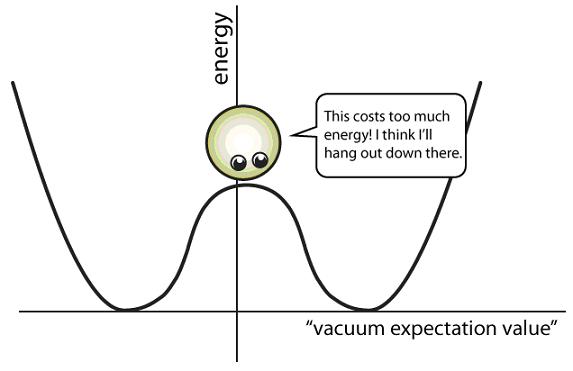
The solid line is a one-dimensional version of the Higgs potential. The x-axis represents the Higgs ”vacuum expectation value,” or vev. For any value other than zero, this means that the Higgs field is “on” at every point in spacetime, allowing fermions to bounce off of it and hence become massive. The y-axis is the potential energy cost of the Higgs taking a particular vacuum value—we see that to minimize this energy, the Higgs wants to roll down to a non-zero vev.

Actually, because the Higgs vev can be any complex number, a more realistic picture is to plot the Higgs potential over the complex plane:

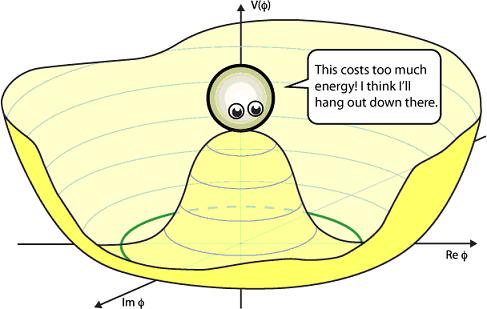
Now the minimum of the potential is a circle and the Higgs can pick any value. Higgs particles are quantum excitations—or ripples—of the Higgs field. Quantum excitations which push along this circle are called Goldstone bosons, and these represent the parts of the Higgs which are eaten by the gauge bosons. Here’s an example:

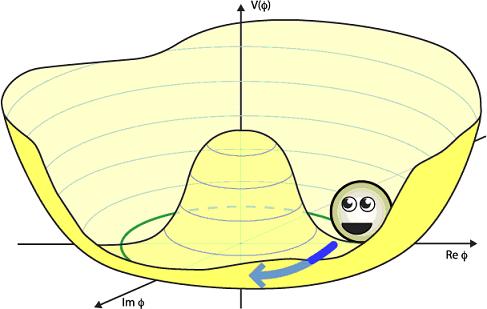
Of course, in the Standard Model we know there are three Goldstone bosons (one each for the W+, W-, and Z), so there must be three “flat directions” in the Higgs potential. Unfortunately, I cannot fit this many dimensions into a 2D picture. The remaining Higgs particle is the excitation in the not-flat direction:

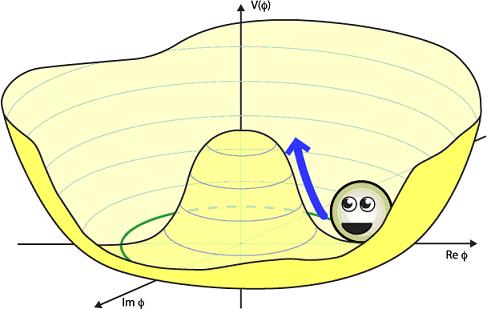
Usually all of this is said rather glibly:

The Higgs boson is the particle which is responsible for giving mass.

A better reason for why we need the Higgs

The above story is nice, but you would be perfectly justified if you thought it sounded like a bit of overkill. Why do we need all of this fancy machinery with Goldstone bosons and these funny “Mexican hat” potentials? Couldn’t we have just had a theory that started out with massive gauge bosons without needing any of this fancy “electroweak symmetry breaking” footwork?

It turns out that this is the main reason why we need the Higgs-or-something-like it. It turns out that if we tried to build the Standard Model without it, then something very nefarious happens. To see what happens, we’ll appeal to some Feynman diagrams, which you may want to review if you’re rusty.

Suppose you wanted to study the scattering of two W bosons off of one another. In the Standard Model you would draw the following diagrams:

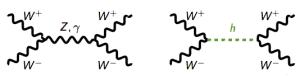
There are other diagrams, but these two will be sufficient for our purposes. You can draw the rest of the diagrams for homework, there should be three more that have at most one virtual particle. In the first diagram, the two W bosons annihilate into a virtual Z boson or a photon (γ) which subsequently decay back into two W bosons. In the second diagram it’s the same story, only now the W bosons annihilate into a virtual Higgs particle.

Recall that these diagrams are shorthand for mathematical expressions for the probability that the Wbosons to scatter off of one another. If you always include the sum of the virtual Z/photon diagrams with the virtual Higgs diagram, then everything is well behaved. On the other hand, if you ignored the Higgs and only included the Z/photon diagram, then the mathematical expressions do not behave.

By this I mean that the probability keeps growing and growing with energy like the monsters that fight the Power Rangers. If you smash the two W bosons together at higher and higher energies, the number associated with this diagram gets bigger and bigger. If these numbers get too big, then it would seem that probability isn’t conserved—we’d get probabilities larger than 100%, a mathematical inconsistency. That’s a problem that not even the Power Rangers could handle.

Mathematics doesn’t actually break down in this scenario—what really happens in our “no Higgs” theory is something more subtle but also disturbing: the theory becomes non-perturbative (or “strongly coupled”). In other words, the theory enters a regime where Feynman diagrams fail. The simple diagram above no longer accurately represents the W scattering process because of large corrections from additional diagrams which are more “quantum,” i.e. they have more unobserved internal virtual particles. For example:

In addition to this diagram we would also have even more involved diagrams with even more virtual particles which also give big corrections:

And so forth until you have more diagrams than you can calculate in a lifetime (even with a computer!). Usually these “very quantum” diagrams are negligible compared to the simpler diagrams, but in the non-perturbative regime each successive diagram is almost as important as the previous. Our usual tools fail us. Our “no Higgs theory” avoids mathematical inconsistency, but at the steep cost of losing predictivity.

Now let me be totally clear: there’s nothing “wrong” with this scenario… nature may very well have chosen this path. In fact, we know at least one example where it has:the theory of quarks and gluons (QCD) at low energies is non-perturbative. But this is just telling us that the “particles” that we see at those energies aren’t quarks and gluons since they’re too tightly bound together: the relevant particles at those energies are mesons and baryons (e.g.pions and protons). Even though QCD—a theory of quarks and gluons—breaks down as a calculational tool, nature allowed us to describe physics in terms of perfectly well behaved (perturbative) “bound state” objects like mesons in aneffective theory of QCD. The old adage is true: when nature closes a door, it opens a window.

So if we took our “no Higgs” theory seriously, we’d be in an uncomfortable situation. The theory at high energies would become “strongly coupled” and non-perturbative just like QCD at low energies. It turns out that for W boson scattering, this happens at around the TeV scale, which means that we should be seeing hints of the substructure of the Standard Model electroweak gauge bosons—which we do not. (Incidentally, the signatures of such a scenario would likely involve something that behaves somewhat like the Standard Model Higgs.)

On the other hand, if we had the Higgs and we proposed the “electroweak symmetry breaking” story above, then this is never a problem. The probability for W boson scattering doesn’t grow uncontrollably and the theory remains well behaved and perturbative.

GOLDSTONE LIBERATION AT HIGH ENERGIES

The way that the Higgs mechanism saves us is somewhat technical and falls under the name of theGoldstone Boson Equivalence Theorem. The main point is that our massive gauge bosons—the ones which misbehave if there were no Higgs—are actually a pair of particles: a massless gauge boson and a massless Higgs/Goldstone particle which was “eaten” so that the combined particle is massive. One cute way of showing this is to show the W boson eating Gold[stone]fish:

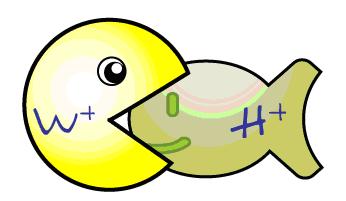
Indeed, at low energies the combined “massless W plus Goldstone” particle behaves just like a massiveW. A good question right now is “low compared to what?” The answer is the Higgs vacuum expectation value (vev), i.e. the energy scale at which electroweak symmetry is broken.

However, at very high energies compared to the Higgs vev, we should expect these two particles to behave independently again. This is a very intuitive statement: it would be very disruptive if your cell phone rang at a “low energy” classical music concert and people would be very affected by this; they would shake their heads at you disapprovingly. However, at a “high energy” heavy metal concert, nobody would even hear your cell phone ring.

Thus at high energies, the “massless W plus Goldstone” system really behaves like two different particles. In a sense, the Goldstone is being liberated from the massive gauge boson:

Now it turns out that the massless W is perfectly well behaved so that at high energies. Further, the set of all four Higgses together (the three Goldstones that were eaten and the Higgs) are also perfectly well behaved. However, if you separate the four Higgses, then each individual piece behaves poorly. This is fine, since the the four Higgses come as a package deal when we write our theory.

What electroweak symmetry breaking really does is that it mixes up these Higgses with the massless gauge bosons. Since this is just a reshuffling of the same particles into different combinations, the entire combined theory is still well behaved. This good behavior, though, hinges on the fact that even though we’ve separated the four Higgses, all four of them are still in the theory.

This is why the Higgs (the one we’re looking for) is so important: the good behavior of the Standard Model depends on it. In fact, it turns out that any well behaved theory with massive gauge bosons must have come from some kind of Higgs-like mechanism. In jargon, we say that the Higgs unitarizes longitudinal gauge boson scattering.

For advanced readers: What’s happening here is that the theory of a complex scalar Higgs doublet is perfectly well behaved. However, when we write the theory nonlinearly (e.g. chiral perturbation theory, nonlinear sigma model) to incorporate electroweak symmetry breaking, we say something like: H(x) = (v+h(x)) exp (i π(x)/v). The π’s are the Goldstone bosons. If we ignore the Higgs, h, we’re doing gross violence to the well behaved complex scalar doublet. Further, we’re left with a non-renormalizable theory with dimensionful couplings that have powers of 1/v all over the place. Just by dimensional analysis, you can see that scattering cross sections for these Goldstones (i.e. the longitudinal modes of the gauge bosons) must scale like a positive power of the energy. In this sense, the problem of “unitarizing W boson scattering” is really the same as UV completing a non-renormalizable effective theory. [I thank Javi S. for filling in this gap in my education.]

CAVEAT: HIGGS VERSUS HIGGS-LIKE

I want to make one important caveat: all that I’ve argued here is that we need something to play the role ofthe Higgs in order to “restore” the “four well behaved Higgses.” While the Standard Model gives a simple candidate for this, there are other theories beyond the Standard Model that give alternate candidates. For example, the Higgs itself might be a “meson” formed out of some strongly coupled new physics. There are even “Higgsless” theories in which this “unitarization” occurs due to the exchange of new gauge bosons. But the point is that there needs to be something that plays the role of the Higgs in the above story.

Why do we expect a Higgs boson?

ELECTROWEAK SYMMETRY IS BROKEN

ELECTROWEAK SYMMETRY IS BROKEN SPONTANEOUSLY

DO WE REALLY NEED A HIGGS?

Why do we expect a Higgs boson? Part II: Unitarization of Vector Boson Scattering

GOLDSTONE LIBERATION AT HIGH ENERGIES

CAVEAT: HIGGS VERSUS HIGGS-LIKE