Source: http://www.redorbit.com/news/science/1586017/the_day_the_world_didnt_end

LHC Images - click on thumbnail for larger image
[Full CERN collection here]

Tunnel Schematic

Tunnel for real - sector 81

Tunnel for real - sector 81

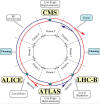
Overview schematic
shows the four main experiments and the two ring structure of the LHC

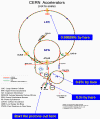
Overview of CERN's acclerator layout

The key element - the 1232 dipoles bend the beam around te 27 km circumference

Joining things up
Once in place the magnet have to be connect - a very complicated task.

Views of tunnel - mostly empty!

3d images from Peter McCready (Atlas and the ring)

Source: http://lhc-machine-outreach.web.cern.ch/lhc-machine-outreach/lhc_in_pictures.htm

Micro Black Holes

Black holes are fascinating! They merge together completely different fields of physics: From General Relativity overthermodynamics and quantum field theory, they do now also reach into the regime of particle and collider physics.

As explained in the intro about extra dimensions, in the presence of additional large compactified dimensions, it would be possible to produce tiny black holes at future colliders. In this case, we would be able to experimentally test Planck scale physics and the onset of quantum gravity with the Large Hadron Collider (LHC), which is scheduled to start next summer. The formation of black holes is a fairly robust prediction and one of the most general expectations that one can have, even though the details are still subject to research. For me, it is quite amazing to see how this field has evolved during the last decade. Starting from a smiled upon speculation, it has by now become a widely accepted scenario for physics beyond the standard model, which is included in simulations of LHC events.

• 1. Micro Black holes in Large Extra Dimensions

• 2. Production of Micro Black Holes

• 3. Evaporation of Micro Black Holes

• 4. Observables of Micro Black Holes

• 5. Further Reading

2. Production of Black Holes

 The production of a black hole in a high energy collision is probably the most inelastic process one might think of. Since the black hole is not an ordinary particle of the standard model, and its correct quantum theoretical treatment is unknown, it is commonly treated as a metastable state, which is produced and decays according to the semi-classical formalism of black hole physics. To compute the production details, the cross-section of the black holes can be approximated by the classical geometric cross-section Pi R². A common approach to improve the naive picture of colliding point particles is to treat the creation of the horizon as a collision of two shock fronts in an Aichelburg-Sexl geometry describing the fast moving particles.

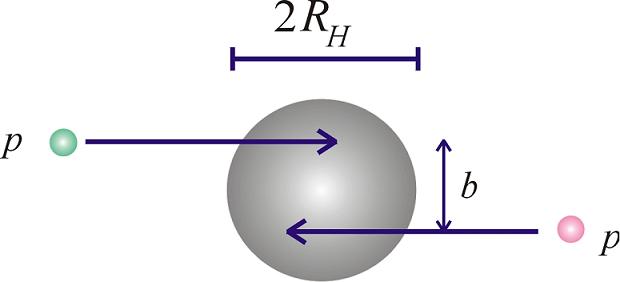
Looking at the figure on the left, we also see that, due to conservation laws, the angular momentum of the formed object only vanishes in completely central collisions with zero impact parameter. In the general case, we will have an angular momentum, and the black hole might also carry an electric charge.

Another assumption which goes into the production details is the existence of a threshold for the black hole formation. From general relativistic arguments, two point like particles in a head on collision with zero impact parameter (the b in the figure above) will always form a black hole, no matter how large or small their energy. At small energies however, we expect this to be impossible due to the smearing of the wave functions by the uncertainty relation. This then results in a necessary minimal energy to allow for the required close approach. This threshold is of order of the new fundamental scale, though the exact value is unknown since quantum gravity effects should play an important role for the wave functions of the colliding particles. Using the geometrical cross section formula, it is now possible to compute the differential and total cross sections for black hole production. This also allows us to estimate the total number of black holes, that would be created at the LHC per year. Inserting the expected technical details for the collider, one finds a number of approximately 10⁹ created black holes per year! This means, about one black hole per second.

3. Evaporation of Black Holes

1. Balding phase: In this phase the black hole radiates away the multipole moments it has inherited from the initial configuration, and settles down in a hairless state. During this stage, a certain fraction of the initial mass will be lost in gravitational radiation.

2. Evaporation phase: The evaporation phase starts with a spin down phase in which the Hawking radiation carries away the angular momentum, after which it proceeds with emission of thermally distributed quanta until the black hole reaches Planck mass. The radiation spectrum contains all Standard Model particles, which are emitted on our brane, as well as gravitons, which are also emitted into the extra dimensions. It is expected that most of the initial energy is emitted in during this phase in Standard Model particles.

3. Planck phase: Once the black hole has reached a mass close to the Planck mass, it falls into the regime of quantum gravity and predictions become increasingly difficult. It is generally assumed that the black hole will either completely decay in some last few Standard Model particles or a stable remnant will be left, which carries away the remaining energy.

To perform a realistic simulation of the evaporation process, one has to take into account the various particles of the standard model with the corresponding degrees of freedom and spin statistics. In the extra dimensional scenario, standard model particles are bound too our submanifold whereas the gravitons are allowed to enter all dimensions. For a precise calculation one also has to take into account that the presence of the gravitational field will modify the radiation properties for higher angular momenta through backscattering at the potential well. These energy dependent greybody factors can be calculated by analyzing the wave equation in the higher dimensional spacetime and the arising absorption coefficients. A very thorough description of these evaporation characteristics has been given by Kanti in 2004 which confirms the expectation that the bulk/brane evaporation rate is of comparable magnitude but the brane modes dominate.

One of the primary observables in high energetic particle collisions is the transverse momentum of the outgoing particles, p_T(pee-tee), the component of the momentum transverse to the direction of the beam. Two colliding partons with high energy can produce a pair of outgoing particles, moving in opposite directions with high p_T but carrying a color charge, as depicted in the figure to the right.

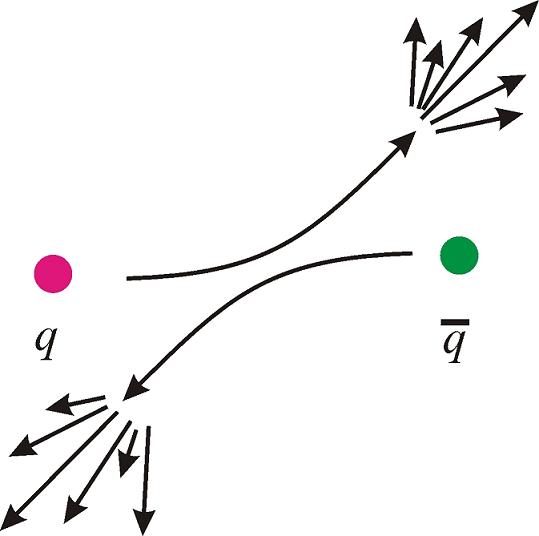
Due to the quark confinement, the color has to be neutralized. This results in a shower of several bound states, the hadrons, which includes mesons (consisting of a quark and an antiquark, like the pions) as well as baryons (consisting of three quarks, like the neutron or the proton). The number of these produced hadrons and their energy depends on the energy of the initial partons. This process will cause a detector signal with a large number of hadrons inside a small opening angle. Such an event is called a jet.

Due to the high energy captured in the black hole, the decay of such an object is a very spectacular event with a distinct signature. The number of decay products, the multiplicity, is high compared to standard model processes and the thermal properties of the black hole will yield a high sphericity of the event. 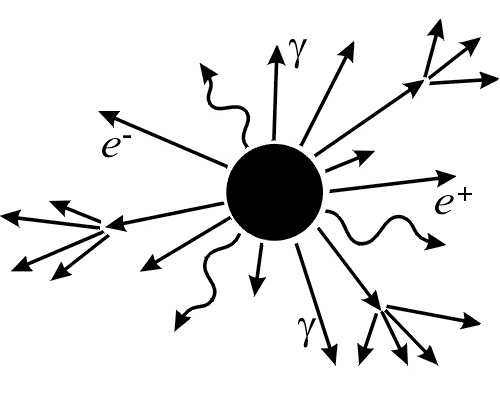Furthermore, crossing the threshold for black hole production causes a sharp cut-off for high energetic jets as those jets now end up as black holes instead, and are re-distributed into thermal particles of lower energies. Thus, black holes will give a clear signal. A schematic picture of this process is shown on the left.

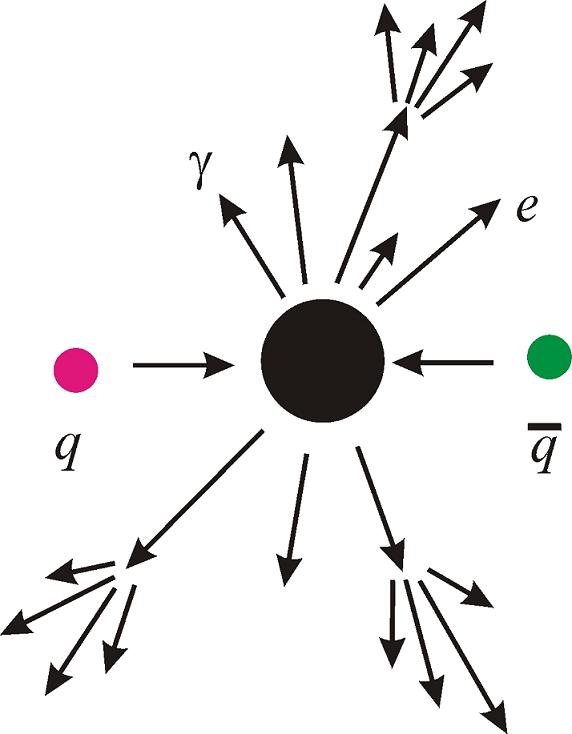
It is apparent that the consequences of black hole production are quite disastrous for the future of collider physics! Once the collision energy crosses the threshold for black hole production, no further information about the structure of matter at small scales can be extracted. As it was put by Giddings and Thomas, this would be ''the end of short distance physics''

By now, several experimental groups include black holes into their search for physics beyond the standard model. Ideally, the energy distribution of the decay products allows a determination of the temperature (by fitting the energy spectrum to the predicted shape) as well as of the total mass of the object (by summing up all energies). This then allows to reconstruct the fundamental scale, and the number of extra dimensions. The quality of the determination depends on the uncertainties in the theoretical prediction as well as on the experimental limits e.g. background from standard model processes. Besides the formfactors of black hole production and the greybody factors of the evaporation, the largest theoretical uncertainties turnout to be the final decay and the time variation of the temperature. In case the black hole decays very fast, it can be questioned whether it has time to readjust its temperature at all or whether it essentially decays completely with its initial temperature. Also, the determination of the properties depends on the number of emitted particles. The less particles, the more difficult the analysis

However, in my opinion the most crucial uncertainty are the latest stages of the evaporation. For hadron colliders like the LHC, the last stages with black hole masses close by the production threshold will dominate the signature, since most of the black holes are actually produced out of parton collisions with a total center-of-mass energy close by even this threshold. In hadronic collisions there are thus very little black holes which actually capture the total available energy of 14 TeV, since the proton's energy gets distributed on its constituents. Such a problem would not be present for a lepton collider.

Source: