To measure anything we need to define units. If I measure in feet
and you measure in meters, we cannot share our results unless
we also know how to convert from one unit to the other.
As scientists first began to understand physics they introduced
separate types of units for each type of quantity they sought to
measure -- so we have units of mass, length, and time, but also units
of heat (calories), electric
charge,
electric current, temperature, pressure etc.
Then as relationships between quantities began to be understood,
the number of separate units decreased. For example, if we know heat
is a form of energy, and we know (from kinetic energy) that energy has
units of mass x length2 x sec-2, then we no
longer need a separate unit for heat.
The laws of thermodynamics took this a step further and related
temperature to heat via the fundamental constant k that
appears in Boltzman's equation. The kinetic energy per atom in an
ideal monoatomic gas at temperature T is E = 3/2 kT,
so clearly the constant k has units of energy over
temperature. It is a fundamental constant of nature, but its numerical
value depends on the units we use for energy and temperature. We
could, but do not usually, choose to use units for temperature that
match the units for energy so that Boltzmann's constant k is
equal to 1.
Two more fundamental constants of nature appear in modern theory,
the speed of light (c) in relativity and Planck's constant (h)
in quantum theory. Each of these has a numerical value that depends on
our units. However, the crucial point is that they give relationships
between quantities which, in classical physics, have completely
different units:
- c relates mass to energy in Einstein's famous
equation E=mc2.
- h relates energy to frequency in Planck's
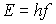 .
.
Further, the understanding of the particulate nature of matter
removes the need for units of charge, instead one just counts the
number of
electron
charges. In other words, nature gives us a fundamental unit of charge.
The units we use should be of a size that makes sense for the
particular subject at hand. It is easiest to define units in each area
of science, and then relate them to one another rather than to go
around measuring particle masses in grams or cheese in proton mass
units.
In particle physics, the standard unit is the unit of energy
GeV. One
eV
(electron Volt) is the amount of energy that an electron gains when it
moves through a potential difference of 1 Volt (in a vacuum). G
stands for Giga, or 109. Thus a GeV is a billion (in US
counting) electron Volts. The mass-energy of a proton or neutron (at
rest) is approximately 1 GeV.
Having chosen a unit of measure, we can then set h=1 to
define a unit of time and c=1 to define a unit of length.
These are crazily tiny lengths and times for everyday purposes, but we
never talk in terms of these units anyway. The choice is convenient
because we can then ignore all the c's and h's in
all our formulae and talk about energy, momentum, and mass all in GeV
units (actually GeV, GeV/c, and GeV/c2, respectively). All
speeds are expressed in terms of fractions of c.