Another peculiarly quantum property is that the wave-like nature of particles leads to interference effects that violate our usual notions of how probability works. Two processes, which when described in a particle language seem quite distinct, actually represent two different contributions to an overall probability amplitude.

The rule for probability in quantum mechanics is that probability is the square of the absolute value of the relevant probability amplitude.

Two processes that can be distinguished by measurement have separate probabilities, and these probabilities add in the usual way. The peculiarity comes about when the processes are not experimentally distinguishable, despite their different particle-language descriptions.

 

An Example of Particle Interference

For example, consider the following Feynman diagrams. Both represent a process where an electron and a positron collide and an electron and a positron emerge traveling in different directions (what we call a scattering process). 

We can read these diagrams as if they are a pictorial representation of a particle process that starts at the left and ends at the right of the picture.

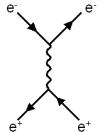	In the first diagram, the electron emits a photon and the positron absorbs it, thus changing the direction of both.
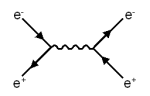	In the second diagram, the electron and positron meet and annihilate, or disappear. For a short time there is only a single virtual photon present, which then disappears to produce a new electron and positron pair, traveling apart in different directions from the initial pair.

These two pictures, and the words we use to "describe" what they represent, certainly appear to be two very different processes. But, we do not observe the intermediate stages and cannot do so without changing the outcome of the experiment.

 

The Mathematics of Interference Calculations

Feynmans prescription assigns a complex number to each diagram, let us write these as A and B. (The values of A and B depend on the momenta and energy of the particles.) The probability of a given scattering occurring is given by |A+B|².

There is no way to say which of the two underlying processes represented by the two diagrams actually occurred. Furthermore, we cannot even say there is a probability of each process and then add the probabilities, since |A+B|² is not the same number as |A|² + |B|² .

For example, let consider A= 5 and B = -3. Then we might think the probability of the process represented by A was |A|²= 25, while that represented by |B|²= 9. Given this, we would be tempted to assign the probability 34 to having either the A or the B process occur -- but the quantum answer is |A+B|² = 2²= 4. That is, the two processes interfere with one another and both contribute to make the net result smaller than it would be if either one alone were the only way to achieve the process!

This is the nature of quantum theories -- unobserved intermediate stages of a process cannot be treated by the ordinary rules of everyday experience.

In both diagrams, the photons that appear at intermediate stages are virtual particles that are not observable.

Quantum Mechanics

Quantum mechanics is the description of physics at the scale of atoms, and the even smaller scales of fundamental particles.

Quantum theory is the language of all particle theories. It is formulated in a well-defined mathematical language. It makes  predictions for the relative probabilities of the various possible outcomes, but not for which outcome will occur in any given case. Interpretation of the calculations, in words and images, often leads to statements that seem to defy common sense -- because our common sense is based on experience at scales insensitive to these types of quantum peculiarities.

Because we do not directly experience objects on this scale, many aspects of quantum behavior seem strange and even paradoxical to us. Physicists worked hard to find alternative theories that could remove these peculiarities, but to no avail.

The word quantum means a definite but small amount. The basic quantum constant h, known as Planck's constant, is 6.626069 x 10^-34 Joule seconds.

Because the particles in high-energy experiments travel at close to the speed of light, particle theories are relativistic quantum field theories.

Lets look at just a few, of the many, quantum concepts that will be stated without explanation.

In quantum theories, energy and momentum have a definite relationship to wavelength. All particles have properties that are wave-like (such as interference) and other properties that are particle-like (such as localization). Whether the properties are  primarily those of particles or those of  waves, depends  on how you observe them.

For example, photons are the quantum particles associated with electromagnetic waves. For any frequency, f, the photons each carry a definite amount of energy (E = hf).

Only by assuming a particle nature for light with this relationship between frequency and particle energy could Einstein explain the photoelectric effect. Conversely, electrons can behave like waves and develop interference patterns.

 

In classical physics, quantities such as energy and angular momentum are assumed to be able to have any value. In quantum physics there is a certain discrete (particle-like) nature to these quantities.

For example, the angular momentum of any system can only come in integer multiples of h/2, where h is Planck's Constant. Values such as (n+1/4)h are simply not allowed.

Likewise, if we ask how much energy a beam of light of a certain frequency, f, deposits on an absorbing surface during any time interval, we find the answer can only be nhf, where n is some integer. Values such as (n+1/2)hf are not allowed.

To get some idea of how counter-intuitive this idea of discrete values is, imagine if someone told you that water could have only integer temperatures as you boiled it. For example, the water could have temperatures of 85º, 86º or 87º, but not 85.7º or 86.5º. It would be a pretty strange world you were living in if that were true.

The world of quantum mechanics is pretty strange when you try to use words to describe it.

 

In quantum mechanics, systems are described by the set of possible states in which they may be found. For example, the electron orbitals familiar in chemistry are the set of possible bound states for an electron in an atom.

Bound states are labeled by a set of quantum numbers that define the various conserved quantities associated with the state. These labels are pure numbers that count familiar discrete quantities, such as electric charge, as well as energy, and angular momentum, which can only have certain discrete values bound quantum systems.

 

A state is described by a quantity that is called a wave-function or probability amplitude. It is a complex-number-valued function of position, that is a quantity whose value is a definite complex number at any point in space. The probability of finding the particle described by the wave function (e.g. an electron in an atom) at that point is proportional to square of the absolute value of the probability amplitude.

The "pictures" of orbitals in an introductory chemistry textbook are a representation of the region within which the wave function gives a high probability of finding an electron for that state.

 

We can also talk about quantum states for freely moving particles. These are states with definite momentum, p, and energy 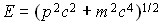.  The associated wave has frequency given by f = pc/h where c is the speed of light.

 

Another peculiarly quantum property is that the wave-like nature of particles leads to interference effects that violate our usual notions of how probability works. Two processes, which when described in a particle language seem quite distinct, actually represent two different contributions to an overall probability amplitude.

The rule for probability in quantum mechanics is that probability is the square of the absolute value of the relevant probability amplitude.

Two processes that can be distinguished by measurement have separate probabilities, and these probabilities add in the usual way. The peculiarity comes about when the processes are not experimentally distinguishable, despite their different particle-language descriptions.

 

An Example of Particle Interference

For example, consider the following Feynman diagrams. Both represent a process where an electron and a positron collide and an electron and a positron emerge traveling in different directions (what we call a scattering process). 

We can read these diagrams as if they are a pictorial representation of a particle process that starts at the left and ends at the right of the picture.

	In the first diagram, the electron emits a photon and the positron absorbs it, thus changing the direction of both.
	In the second diagram, the electron and positron meet and annihilate, or disappear. For a short time there is only a single virtual photon present, which then disappears to produce a new electron and positron pair, traveling apart in different directions from the initial pair.

These two pictures, and the words we use to "describe" what they represent, certainly appear to be two very different processes. But, we do not observe the intermediate stages and cannot do so without changing the outcome of the experiment.

 

The Mathematics of Interference Calculations

Feynmans prescription assigns a complex number to each diagram, let us write these as A and B. (The values of A and B depend on the momenta and energy of the particles.) The probability of a given scattering occurring is given by |A+B|².

There is no way to say which of the two underlying processes represented by the two diagrams actually occurred. Furthermore, we cannot even say there is a probability of each process and then add the probabilities, since |A+B|² is not the same number as |A|² + |B|² .

For example, let consider A= 5 and B = -3. Then we might think the probability of the process represented by A was |A|²= 25, while that represented by |B|²= 9. Given this, we would be tempted to assign the probability 34 to having either the A or the B process occur -- but the quantum answer is |A+B|² = 2²= 4. That is, the two processes interfere with one another and both contribute to make the net result smaller than it would be if either one alone were the only way to achieve the process!

This is the nature of quantum theories -- unobserved intermediate stages of a process cannot be treated by the ordinary rules of everyday experience.

In both diagrams, the photons that appear at intermediate stages are virtual particles that are not observable.